题目内容
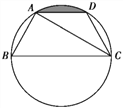
【题目】如图，在△ABC中，∠B=45°，在BC边上取一点D，使CD=CA，点E在AC上，连接ED，若∠AED=45°,且CE=1，BD=2，则AD的长是 ．
【答案】
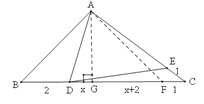
【解析】解：过A作AG⊥BC于G，在CD上截取CF=1，连结AF．∵AC=DC，∠C=∠C，CE=CF，∴△DCE≌△ACF，∴∠DEC=∠AFC，∴∠AFD=∠AED=45°．∵∠B=45°，∴∠B=∠AFD，∴AB=AF，∴BG=FG．设DG=x，则GF=BG=x+2，DC=AC=2x+3．∵∠B=45°，AG⊥BC，∴∠BAG=∠B=45°，∴AG=BG=x+2．GC=x+3．在Rt△AGC中，∵AG2+GC2=AC2，∴ 
，整理得： 
，解得：x=－2（舍去），x=1．∴DG=1，AG=2+x=3，∴AD=
=
=
．故答案为： 
．
练习册系列答案
相关题目
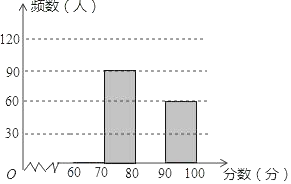
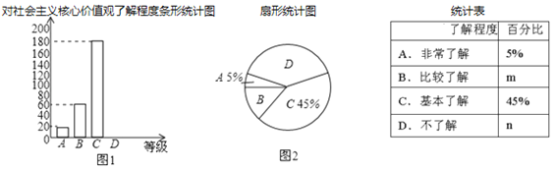
【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题．
组别 | 分数段（分） | 频数 | 百分率（%） |
A组 | 60≤x＜70 | 30 | 10 |
B组 | 70≤x＜80 | 90 | n |
C组 | 80≤x＜90 | m | 40 |
D组 | 90≤x＜100 | 60 | 20 |
（1）样本容量a＝ ，表中m＝ ，n＝ ；
（2）补全频数分布直方图；
（3）若成绩在80分以上（包括80分）为“优”等，请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人？
