题目内容
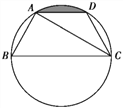
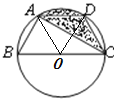
【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
【答案】(1)圆的半径为2;(2)![]() -
-![]()
【解析】试题分析:(1)已知AC平分∠BCD,由角平分线的定义可得∠ACD=∠ACB,
再由AD∥BC,即可得∠ACB=∠DAC=∠ACD,因∠ADC=120°,根据等腰三角形的性质和圆内接四边形互补可得∠ACB=∠DAC=∠ACD =30°,∠B=60°,根据圆周角定理的推论可得AB=AD=DC,且∠BAC=90°,即可BC为直径;设圆心为O,AB=x,则BC=2AB=2x,
由四边形ABCD的周长为10cm,可得x+x+x+2x=10,解得x=2,即可求得⊙O的半径为2;(2)设圆心为O,连接OA、OD,由(1)可知OA=OD=AD,可得△AOD为等边三角形,根据等边三角形的性质可得∠AOD=60°;因AD∥BC,可得![]() ,即可得
,即可得![]() .
.
试题解析:
(1)∵AC平分∠BCD,
∴∠ACD=∠ACB,
又∵AD∥BC,
∴∠ACB=∠DAC=∠ACD,
而∠ADC=120°,
∴∠ACB=∠DAC=∠ACD =30°,∠B=60°,
∴AB=AD=DC,且∠BAC=90°,
∴BC为直径,设圆心为O,AB=x,则BC=2AB=2x,
又∵四边形ABCD的周长为10cm,
∴x+x+x+2x=10,解得x=2,
即⊙O的半径为2.
(2)设圆心为O,连接OA、OD,
由(1)可知OA=OD=AD,
∴△AOD为等边三角形,
∴∠AOD=60°;
∵AD∥BC,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/ | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
则这些运动员成绩的中位数,众数分别为( )
A. 1.65,1.70 B. 1.65,1.75 C. 1.70,1.75 D. 1.70,1.70
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?