题目内容
【题目】如图，在平面直角坐标系中，四边形ABCD的四个顶点分别在函数
与
的图象上，对角线
轴，且
于点
.已知点B的横坐标为4.
（1）当
，
时，
①若点P的纵坐标为2，求四边形ABCD的面积．
②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．
（2）当四边形ABCD为正方形时，直接写出m、n之间的数量关系．
【答案】（1）①
；②四边形ABCD是菱形，见解析；（2）
．
【解析】
（1）①先确定出点A，B，C，D坐标，再利用面积的求法即可得出结论；
②先确定出点D坐标，进而确定出点P坐标，进而求出PA，PC，即可得出结论；
（2）先确定出B（4，
），D（4，
），进而求出点P的坐标，再求出A，C坐标，最后用AC=BD，即可得出结论．
解：（1）①
，
，
，
.
∵点B的横坐标为4，
．
．
轴，
，点P的纵坐标为2，
∴
，
．
．
∴
；
②四边形ABCD是菱形．
理由：
，点P是线段BD的中点，
．
轴，，
∴
．
．
，∴四边形ABCD为平行四边形．
，∴四边形ABCD是菱形．
（2）．
理由：当四边形ABCD是正方形，记AC，BD的交点为P，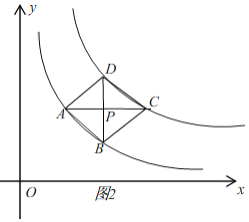
∴BD=AC
当x=4时，y=
=， y=
= ，
∴B（4，），D（4，），
∴P（4，
），
∴A（
， ），C（
，）
∵AC=BD，
∴-=-，
∴m+n=32
故答案为：（1）①；②四边形ABCD是菱形，见解析；（2）．
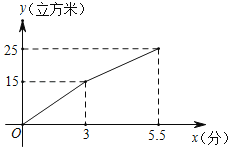
【题目】张先生今年7月份第一个星期的星期五以每股（份）25元的价格买进某种金融理财产品共2000股（买入时免收手续费），该理财产品在第二个星期的五个交易日中，每股的涨跌情况如下表(表格中数据表示比前一交易日涨或跌多少元) (单位：元)：
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌额 |
|
|
|
|
|
（1）写出第二个星期每日每股理财产品的收盘价（即每日最后时刻的成交价）；
（2）已知理财产品卖出时，交易所需收取千分之三的手续费，如果张先生在第二个星期的星期五交易结束前将全部产品卖出，他的收益情况如何?
