题目内容
【题目】如图，点A（2，2）在双曲线y1=
（x＞0）上，点C在双曲线y2=－
（x＜0）上，分别过A、C向x轴作垂线，垂足分别为F、E，以A、C为顶点作正方形ABCD，且使点B在x轴上，点D在y轴的正半轴上．
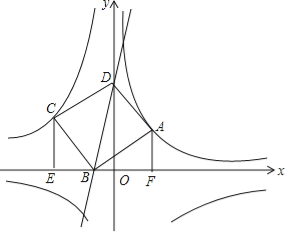
（1）求k的值；
（2）求证：△BCE≌△ABF；
（3）求直线BD的解析式．
【答案】（1)4.（2)证明见解析.（3）y=5x+5．
【解析】
试题（1）把A点坐标代入y1=
可求得k的值；
（2）由正方形的性质得出BC=AB，∠ABC=90°，再由角的互余关系证出∠BCE=∠ABF，由AAS即可证明△BCE≌△ABF；
（3）由△BCE≌△ABF得出BE=AF=2，CE=BF，设OB=x，则OE=x+2，CE=BF=x+2，点C的坐标为：（－x－2，x+2），代入双曲线y2=－
（x＜0）得出方程：－（x+2）2=－9，得出x=1，OB=1，B（－1，0），AG=5，再由HL证明Rt△BOD≌Rt△CGA，得出OD=AG=5，得出D（0，5），设直线BD的解析式为：y=kx+b，把B、D坐标代入得出方程组，解方程组求出k、b，即可得出直线BD的解析式．
试题解析：（1）解：把点A（2，2）代入y1=，
得：2=
，
∴k=4；
（2）证明：∵四边形ABCD是正方形，
∴BC=AB，∠ABC=90°，BD=AC，
∴∠EBC+∠ABF=90°，
∵CE⊥x轴，AF⊥x轴，
∴∠CEB=∠BFA=90°，
∴∠BCE+∠EBC=90°，
∴∠BCE=∠ABF，
在△BCE和△ABF中，
，
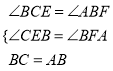∴△BCE≌△ABF；
（3）解：连接AC，作AG⊥CE于G，如图所示：
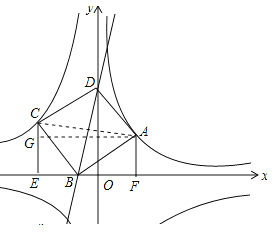
则∠AGC=90°，AG=EF，GE=AF=2，
由（2）得：△BCE≌△ABF，
∴BE=AF=2，CE=BF，
设OB=x，则OE=x+2，CE=BF=x+2，
∴OE=CE，
∴点C的坐标为：（－x－2，x+2），
代入双曲线y2=－（x＜0）得：－（x+2）2=－9，
解得：x=1，或x=－5（不合题意，舍去），
∴OB=1，BF=3，CE=OE=3，
∴EF=2+3=5，CG=1=OB，B（－1，0），AG=5，
在Rt△BOD和Rt△CGA中，
，
∴Rt△BOD≌Rt△CGA（HL），
∴OD=AG=5，
∴D（0，5），
设直线BD的解析式为：y=kx+b，
把B（－1，0），D（0，5）代入得：
，
解得：k=5，b=5．
∴直线BD的解析式为：y=5x+5．
