Question

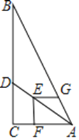
【题目】△ABC中，AC＝BC，∠ACB＝α，点D是平面内不与点A和点B重合的一点，连接DB，将线段DB绕点D顺时针旋转α得到线段DE，连接AE、BE、CD．

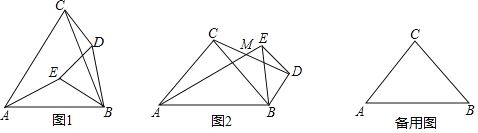
（1）如图①，点D与点A在直线BC的两侧，α＝60°时，的值是　 ；直线AE与直线CD相交所成的锐角的度数是　 度；

（2）如图②，点D与点A在直线BC两侧，α＝90°时，求的值及直线AE与直线CD相交所成的锐角∠AMC的度数；

（3）当α＝90°，点D在直线AB的上方，S△ABD＝S△ABC，请直接写出当点C、D、E在同一直线上时，的值．

Answer 1

【答案】（1）1，60；（2）∠AMC＝45°；（3）的值为2﹣或2+．

【解析】

（1）延长AE，CD交于点H，根据旋转的性质可知DE=BD，∠BDE=60°，从而可知△BDE，从而可证△ABE≌△CBD，从而可知，再根据角的关系即可求出∠AHB；

（2）先证△ABE∽△CBD，可以得到，∠BAE＝∠BCD，继而可以求出∠AMC的度数；

（3）分两种情况讨论即可：①点D，点A在直线BC两侧，②点A，点D在直线BC同侧.

（1）如图1，延长AE，CD交于点H，

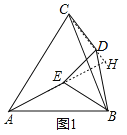
∵将线段DB绕点D顺时针旋转α得到线段DE，

∴DE＝BD，∠BDE＝60°，

∴△BDE是等边三角形，

∴BD＝BE，∠DBE＝60°，

∵△ABC是等边三角形，

∴AB＝BC，∠ABC＝∠DBE＝60°，

∴∠ABE＝∠CBD，且BE＝BD，AB＝BC，

∴△ABE≌△CBD（SAS）

∴AE＝CD，∠DCB＝∠BAE，

∴＝1，

∵∠BAC+∠ACB＝120°，

∴∠BAE+∠CAE+∠ACB＝120°，

∴∠CAE+∠ACB+∠BCD＝120°

∴∠CAE+ACH＝120°，

∴∠AHB＝60°，

故答案为：1，60．

（2）∵AC＝BC，∠ACB＝90°，

∴AB＝BC，∠ABC＝45°，

∵将线段DB绕点D顺时针旋转90°得到线段DE，

∴DE＝BD，∠BDE＝90°，

∴BE＝BD，∠DBE＝45°，

∴∠DBE＝∠ABC，

∴∠ABE＝∠CBD，且，

∴△ABE∽△CBD，

∴，∠BAE＝∠BCD，

∵∠BAC+∠ACB＝135°＝∠ACB+∠CAM+∠BAE，

∴∠ACB+∠CAM+∠BCD＝∠CAM+∠ACM＝135°，

∴∠AMC＝45°；

（3）①若点D，点A在直线BC两侧，如图3，分别取AC，BC中点G，H，连接GH，

∵，

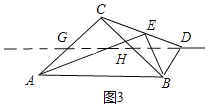
∴点D在直线GH上，

∵∠ACB＝∠BDE＝90°，AC＝BC，DE＝BD，

∴∠CAB＝∠CBA＝45°，∠DEB＝∠DBE＝45°，BE＝BD，

∵点G，点H分别是AC，BC的中点，

∴GH∥AB，

∴∠DHB＝∠ABC＝45°，

∵点C、E、D三点共线，

∴∠CDB＝90°，且点H是BC中点，

∴DH＝CH＝BH，

∴∠HCD＝∠HDC，且∠HCD+∠HDC＝∠BHD＝45°，

∴∠HCD＝∠HDC＝22.5°，

∵∠BED＝∠BCE+∠CBE＝45°，

∴∠BCE＝∠CBE＝22.5°，

∴BE＝CE＝BD，

∴CD＝CE+DE＝（+1）BD，

∴；

②若点A，点D在直线BC同侧，如图4，分别取AC，BC中点G，H，连接GH，

∵，

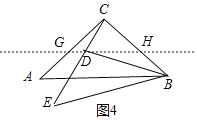
∴点D在直线GH上，

∵∠ACB＝∠BDE＝90°，AC＝BC，DE＝BD，

∴∠CAB＝∠CBA＝45°，∠DEB＝∠DBE＝45°，BE＝BD，

∵点G，点H分别是AC，BC的中点，

∴GH∥AB，

∴∠DHC＝∠ABC＝45°，

∵点C、E、D三点共线，

∴∠CDB＝90°，且点H是BC中点，

∴DH＝CH＝BH，

∴∠HBD＝∠HDB，且∠HBD+∠HDB＝∠CHD＝45°，

∴∠HBD＝∠HDB＝22.5°，

∵∠ECB＝67.5°，∠EBC＝∠EBD+∠DBC＝67.5°，

∴∠BCE＝∠CBE＝67.5°，

∴BE＝CE＝BD，

∴CD＝CE﹣DE＝（﹣1）BD，

∴，

综上所述：的值为或．