Question

【题目】初三某班同学小代想根据学习函数的经验，探究函数的图象和性质，下面是他的探究过程，请补充完整：

（1）函数的自变量的取值范围是 ;

（2）下表是函数与自变量的几组对应值：

		-3	-2	-1	0	1	3	4	5	6	7
		0.6	m	1	1.5	3	n	1.5	1	0.75	0.6

则m= ,n= ；

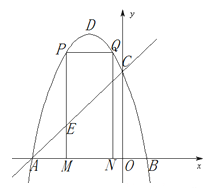
（3）在平面直角坐标系xoy中，补全此函数的图象:

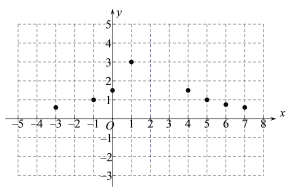
（4）根据函数图象，直接写出不等式的解集 ;

（5）若函数与函数y＝x＋k图象有三个不同的交点，则k的取值范围是 .

Answer 1

【答案】（1）；（2）m=0.75,n= 3；（3）在平面直角坐标系xoy中，补全此函数的图象见解析；（4）；（5）.

【解析】

（1）根据分母不能为0确定自变量的取值范围；

（2）把x=-2,3分别代入可求得m,n的值；

（3）把两组点分别顺次连接可得图象；

（4）作出函数y=x-2的图象，得直线与的交点的横坐标为x=2+.根据图象可得到不等式的解集；

（5）直线y=x+k与右边曲线总有一个交点，故可求当直线与左边曲线有一个交点时k的值，将直线向上平移就会满足题中有三个交点的条件，从而得到k的取值范围.

（1）根据分母不能为0得│x-2│≠0，解得： ；

（2）将x=-2代入，得y=0.75,即m=0.75;

将x=3代入，得y=3,即n=3;

故答案为：m= 0.75 ,n= 3 ；

（3）如图所示:

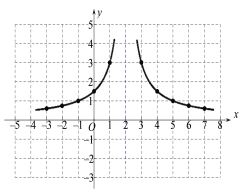
（4）如图，作出函数y=x-2的图象，这条直线与的交点的横坐标为x=2+.

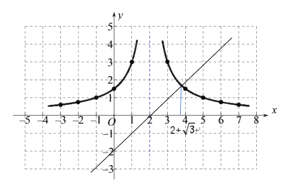
观察图象可得，不等式的解集为或.

（5）由（4）的结论可知，直线y=x+k与的图象的右边的曲线总有一个交点，故考虑当x＜2时，直线y=x+k与的图象的左边的曲线的交点情况.

∵x＜2,∴，列方程＝x+k，

整理得，

当时，方程有唯一解，直线与左边曲线有一个交点，直线继续往上平移，会有两个交点.

∴

解得 (由图像知不合题意舍去)

所以当时，直线y=x+k与共有三个不同的交点.

故答案为：.