Question

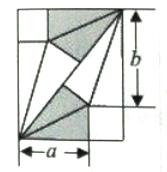
【题目】我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理，如图所示的长方形由两个这样的图形拼成，若，，则该长方形的面积为__________.

Answer 1

【答案】

【解析】

欲求矩形的面积，则求出小正方形的边长即可；设小正方形的边长为x，已知a=3，b=4，得AB=3+4=7，在Rt△ABC中，AC2+BC2=AB2，即(3+x)2+(x+4)2=72；

整理得x2+7x-12=0，解方程求出x的值，进而可求出该矩形的面积.

如图.

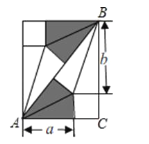
设小正方形的边长为x，

∵a=3，b=4，

∴AB=3+4=7.

在Rt△ABC中，AC2+BC2=AB2，

即(3+x)2+(x+4)2=72，

整理得，x2+7x-12=0，

解得，或（舍去），

∴该矩形的面积

故答案为：.