题目内容
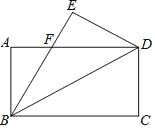
【题目】如图1,在△ABC中,AB=AC=4,∠ABC=67.5°,△ABD和△ABC关于AB所在的直线对称,点M为边AC上的一个动点(重合),点M关于AB所在直线的对称点为N,△CMN的面积为S.
(1)求∠CAD的度数;
(2)设CM=x,求S与x的函数表达式,并求x为何值时S的值最大?
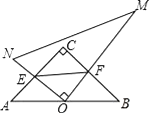
(3)S的值最大时,过点C作EC⊥AC交AB的延长线于点E,连接EN(如图2),P为线段EN上一点,Q为平面内一点,当以M,N,P,Q为顶点的四边形是菱形时,请直接写出所有满足条件NP的长.
【答案】(1)∠CAD=90°;(2)S=﹣![]() x2+2x,当x=2时,S有最大值.(3)2
x2+2x,当x=2时,S有最大值.(3)2![]() 或2
或2![]() 或
或![]() .
.
【解析】分析:(1)由三角形的内角和定理可得∠BAC,再由轴对称的性质求∠CAD;(2)AM=4-x,又△AMN是等腰直角三角形,由三角形的面积公式和二次函数的性质即可求解;(3)用勾股定理求出AE,AO,ON,OE,EN的长,因为点M,N不动,点P,Q是动点,所以需要分三种情况讨论,分别画出每一种情况的图形,根据图形求解.
详解:(1)∵AB=AC,∠ABC=67.5°,
∴∠ACB=∠ABC=67.5°,∴∠CAB=180°﹣67.5°﹣67.5°=45°,
∵△ABD和△ABC关于AB所在的直线对称,
∴∠DAB=∠CAB=45°,
∴∠CAD=45°+45°=90°.
(2)由(1)知:AN⊥AM,
∵点M.N关于AB所在直线对称,∴AM=AN,
∵CM=x,∴AN=AM=4﹣x,
∴S=![]() ×CM×AN=
×CM×AN=![]() x(4﹣x),
x(4﹣x),
∴S=﹣![]() x2+2x,
x2+2x,
∴当x=﹣![]() =2时,S有最大值.
=2时,S有最大值.
(3)∵CE⊥AC,
∴∠ECA=90°,∵∠CAB=45°,
∴∠CEA=∠EAC=45°,∴CE=AC=4,
在Rt△ECA中,AC=EC=4,由勾股定理得:EA=![]() ,
,
∵AM=AN,∠CAB=∠DAB,∴AO⊥MN,MO=NO,
在Rt△MAN中,AM=AN=4﹣2=2,由勾股定理得:MN=![]() ,
,
∴MO=NO=![]() ,
,
由勾股定理得:AO=![]() ,
,
∴EO=4![]() ﹣
﹣![]() ,
,
在Rt△EON中,EO=![]() ,NO=
,NO=![]() ,
,
由勾股定理得:EN=![]() ,
,
分为三种情况:①当以MN为对角线时,此时P在E上,即NP=NE=![]() ;
;
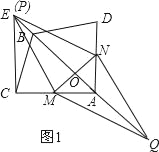
②以MN为一边时,以N为圆心,以MN为半径画弧交NE于P,
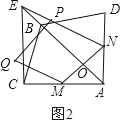
此时NP=MN=![]() ;
;
③以MN为一边时,
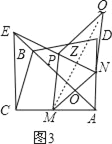
过M作MZ⊥NE于Z,则PZ=NZ,
∵AE⊥MN,∴∠EON=∠MZN=90°,
∵∠ENO=∠MNZ,∴△ENO∽△MNZ,
∴![]() ,∴
,∴![]() ,
,
∴ZN=![]() ,∴NP=2ZN=
,∴NP=2ZN=![]() .
.
即所有满足条件NP的长是![]() 或
或![]() 或
或![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案【题目】数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.

下面是探究过程,请补充完整:
(1)设小正方形的边长为x dm,体积为y dm3,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(3)列出y与x的几组对应值.
x/dm | … |
|
|
|
|
|
|
|
|
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | m | 3.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | … |
(4)在下面的平面直角坐标系![]() 中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
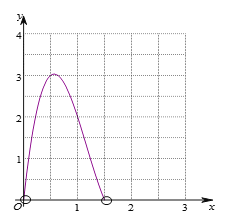
结合画出的函数图象,解决问题:
当小正方形的边长约为 dm时,(保留1位小数),盒子的体积最大,最大值约为 dm3.(保留1位小数)
【题目】某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲 | 85 | 88 | 84 | 85 | 83 |
乙 | 83 | 87 | 84 | 86 | 85 |
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.