题目内容
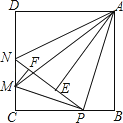
【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

【答案】(1)见解析;(2)25°
【解析】
(1)根据SAS即可证明;
(2)在△ABE中,求出∠A,∠ABE即可解决问题.
(1)证明:∵∠1=∠2,
∴∠1+∠EBF=∠2+∠EBF,
即∠ABE=∠CBF.
在△ABE和△CBF中,∵
∴△ABE≌△CBF.
(2)∵∠1=∠2,∠FBE=40°,
∴∠1=∠2=70°.
∵△ABE≌△CBF,
∴∠A=∠C=45°,
∵∠ABE=∠1+∠FBE=70°+40°=110°,
∴∠E=180°-∠A-∠ABE=180°-45°-110°=25°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目