题目内容
如图，在△ABC中，AB=AC，AE是角平分线，AD是△ABC外角∠CAG的平分线，CF⊥AD于F．
（1）试说明四边形AECF为矩形；
（2）当△ABC满足什么条件时，四边形AECF是一个正方形？请说明理由．
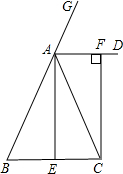
（1）试说明四边形AECF为矩形；
（2）当△ABC满足什么条件时，四边形AECF是一个正方形？请说明理由．
（1）因为∠BAE=∠CAE，∠GAD=∠CAD，
所以2（∠CAE+∠CAD）=180°，
所以∠CAE十∠CAD=90°，
即∠EAD=90°，
因为AB=AC，AE是角平分线，
所以AE⊥BC，
由于CF⊥AD，
所以四边形AECF是矩形．
（2）当∠BAC=90°，即△ABC是直角三角形时，四边形AECF是正方形，
理由：由于∠BAC=90°，
所以∠CAE=45°，
所以∠CAD=45°，
因为∠AEC=∠AFC=90°，AC=AC，
所以△AEC≌△AFC，
所以AE=AF，
所以四边形AECF是正方形．
所以2（∠CAE+∠CAD）=180°，
所以∠CAE十∠CAD=90°，
即∠EAD=90°，
因为AB=AC，AE是角平分线，
所以AE⊥BC，
由于CF⊥AD，
所以四边形AECF是矩形．
（2）当∠BAC=90°，即△ABC是直角三角形时，四边形AECF是正方形，
理由：由于∠BAC=90°，
所以∠CAE=45°，
所以∠CAD=45°，
因为∠AEC=∠AFC=90°，AC=AC，
所以△AEC≌△AFC，
所以AE=AF，
所以四边形AECF是正方形．
练习册系列答案
考前必练系列答案
相关题目
直角的一边始终经过点B，另一边与射线DC相交于Q．
