Question

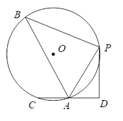
【题目】如图，在⊙O中，B，P，A，C是圆上的点，， PD⊥CD，CD交⊙O于A，若AC=AD，PD = ，sin∠PAD = ，则△PAB的面积为_______．

Answer 1

【答案】2

【解析】分析：在Rt△PAD中，计算得出AD＝1，连接PC、PB、PA，过P作BA垂线于H点，由得到PB=PC，再由全等三角形的判定定理可得出△PBH≌△PCD，Rt△PHA≌Rt△PDA，再得出AC=AD=1，PH=PD＝，再由计算得出结论．

详解：

∵PD⊥CD，PD = ，sin∠PAD = ，sin∠PAD＝，

∴AP＝，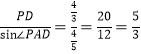

∴AD＝，

连接PC、PB、PA，过P作BA垂线于H点，如图所示：

∵ ，

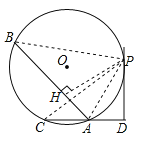
∴PB=PC

∴∠B=∠C，∠PHB=∠PDA，
∴∠BPH=∠DPC，
在△PBH与△PCD中，

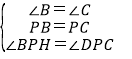
∴△PBH≌△PCD（ASA），
∴BH=CD=2，PH=PD，
在Rt△PHA与Rt△PDA中，

∴Rt△PHA≌Rt△PDA（HL），
∴HA=AD=1
∴AB=BH+HA=3．

∴△PAB的面积为.

故答案是：2.