��Ŀ����
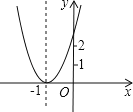
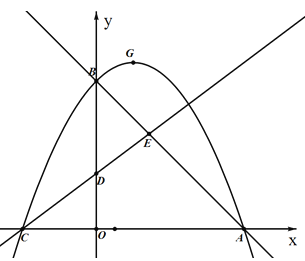
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������ֽy=ax2+bx+c��x�ύ�ڵ�A,C����y�ύ�ڵ�B.��֪��A����Ϊ(8��0)����BΪ(0��8)����DΪ��0��3����tan��DCO=![]() ��ֱ��AB��ֱ��CD�ཻ�ڵ�E.
��ֱ��AB��ֱ��CD�ཻ�ڵ�E.
�� �������ߵĽ���ʽ��������y=a(x-m)2+h����ʽ��
�� �������ߵĶ���ΪG������ֱ��AB�Ϸ��������������P�����꣬ʹ��S��ABP=S��ABG.
�� ��MΪֱ��AB�ϵ�һ�㣬����M��x���ƽ���߷ֱ�ֱ��AB��CD�ڵ�M��N������DM��DN���Ƿ���ڵ�M��ʹ����DMNΪ���������Σ������ڣ��������M�����ꣻ�������ڣ���˵������.
���𰸡���1��![]() ����2��M��20��-12����M��
����2��M��20��-12����M��![]() ��
�� ![]() ���� M��-
���� M��-![]() ��
�� ![]() ��
��
�������������������1����Rt��DOC�У������пɵõ�C���꣬�������ߵĽ���ʽΪ![]() ���ѵ�B������룬��a��ֵ�����ɵ������߽���ʽ���ٻ�Ϊ����ʽ���ɣ�
���ѵ�B������룬��a��ֵ�����ɵ������߽���ʽ���ٻ�Ϊ����ʽ���ɣ�
��2�����P���꣬����P��PF��y�ύֱ��AB��F����AB������ɵó�ֱ��AB�Ľ���ʽ��
�ɴ˵�PF ,����G��GH��y�ύֱ��AB��H����GH=3����PF= GH=3�����xֵ��������õ�P���ꣻ
��3��������������ٵ�DM=DNʱ����DN=MNʱ�����M��ֵ����.
�����������1����Rt��DOC���� ![]() ����
����![]() ��
��
��OC=4 ��
��C(-4��0)��
��![]() ���ѵ�B��0,8�����룬��
���ѵ�B��0,8�����룬��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
��2����P��x�� ![]() ��������P��PF��y�ύֱ��AB��F��
��������P��PF��y�ύֱ��AB��F��
�� A��8,0����B��0,8��
��![]()
��F��x,-x+8��
��PF=![]() ��
��
����G��GH��y�ύֱ��AB��H����G��2,9����H��2,6��
��GH=3��
��PF= GH=3��
��![]() =3��
=3��
���![]() ����ȥ��
����ȥ��
��P��6,5����
��3����1�������
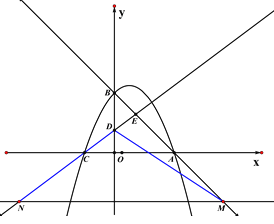
��DM=DNʱ��M��20��-12����
��M��m��-m+8������N��-m�� ![]() ����
����
��MN��x�ᣬ
�� -m+8=![]() ��
��
��m=20��
��2�������

��DN=MNʱ��M![]() M
M![]() ��
��
��M��m��-m+8������N��![]() ��-m+8����
��-m+8����
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() .
.

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�