题目内容
【题目】下图是投影仪安装截面图.教室高EF=3.5 m,投影仪A发出的光线夹角∠BAC=30°,投影屏幕高BC=1.2 m.固定投影仪的吊臂AD=0.5 m,且AD⊥DE,AD∥EF,∠ACB=45°.求屏幕下边沿离地面的高度CF(结果精确到0.1 m).
(参考数据:tan15°≈0.27,tan30°≈0.58)

【答案】1.4m
【解析】分析:过点A作AP⊥EF,垂足为P,可证明四边形ADEP为矩形,再求得∠BAP=15° ,AP=CP,在Rt△APB中,根据锐角三件函数可得BP=0.27AP=0.27CP,再由BC=CP—BP求得CP的长,即可求得CF的长.
详解:
过点A作AP⊥EF,垂足为P,

∵AD⊥DE,∴∠ADE=90°,
∵AD∥EF,∴∠DEP=90°,
∵AP⊥EF,
∴∠APE=∠APC=90°,
∴∠ADE=∠DEP=∠APE=90°,
∴四边形ADEP为矩形,
∴EP=AD=0.5m ,∠APC=90°,∠ACB=45°,
∴∠CAP=45°=∠ACB,∠BAP=∠CAP—∠CAB=45°—30°=15°
∴AP=CP
在Rt△APB中,
tan∠BAP=![]() =tan15°=0.27 ,
=tan15°=0.27 ,
∴BP=0.27AP=0.27CP,
∴BC=CP—BP=CP—0.27CP=0.73CP=1.2m,
∴CP=1.64m,
∴CF=EF—EP—CP=3.5—0.5—1.64=1.36≈1.4m

【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.

成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.
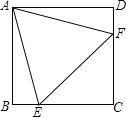
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()