题目内容
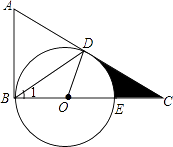
【题目】如图,△ABC中,AB=AC=10,BC=12,点D在边BC上,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交AC或延长线于点F. 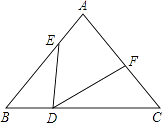
(1)当AE=4时,求AF的长;
(2)当以边AC为直径的⊙O与线段DE相切时,求BE的长.
【答案】
(1)解:∵∠EDF+∠FDC=∠B+∠DEB,∠EDF=∠B,
∴∠FDC=∠DEB,
∵AB=AC,
∴∠C=∠B,
∴△CDF∽△BED,
∴ ![]() ,即
,即 ![]() ,
,
解得:CF= ![]() ,
,
∴AF=AC﹣CF=10﹣ ![]()
(2)解:取边AC中点O,作OG⊥DE于G,OQ⊥BC于Q,过点A作AH⊥BC于H,连接OD,如图所示:
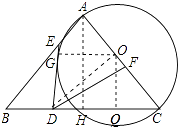
∵AB=AC,AH⊥BC,
∴CH= ![]() BC=6,
BC=6,
∵⊙O和线段DE相切,
∴OG= ![]() AC=5,
AC=5,
在Rt△CAH中,∠AHC=90°,cosC= ![]() ,
,
在Rt△CQO中,∠CQO=90°
∵cosC= ![]() ,
,
∴CQ=COcosC=5× ![]() =3,
=3,
∴DQ=BC﹣BD﹣CQ=12﹣4﹣3=5,
∴OG=DQ,
在Rt△OGD与Rt△DQO中, ![]() ,
,
∴Rt△OGD≌Rt△DQO(HL),
∴∠GOD=∠QDO,
∴OG∥BC,
∴∠EDB=∠OGD=90°,
∴cosB= ![]() =cosC=
=cosC= ![]() ,
,
∴BE= ![]() ,
,
∴当以边AC为直径的⊙O与线段DE相切时,BE= ![]() .
.
【解析】(1)先证△BDE∽△CFD,得出对应边成比例,求出CF的长,即可得出结果;(2)取边AC中点O,作OG⊥DE于G,OQ⊥BC于Q,过点A作AH⊥BC于H,连接OD,则CH= ![]() BC=6,由⊙O和线段DE相切,得出OG=
BC=6,由⊙O和线段DE相切,得出OG= ![]() AC=5,求出cosC=
AC=5,求出cosC= ![]() =
= ![]() ,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL证得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB=
,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL证得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB= ![]() =cosC=
=cosC= ![]() ,即可得出结果.
,即可得出结果.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?