��Ŀ����
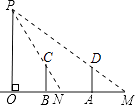
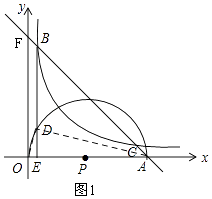
����Ŀ����ͼ����֪y=��x+m��m��4��������A��m��0�������뷴��������y= ![]() ��ͼ����B��C���㣨��B�ڵ�C����ߣ�����OAΪֱ��������������y=
��ͼ����B��C���㣨��B�ڵ�C����ߣ�����OAΪֱ��������������y= ![]() ��ͼ���ཻ�İ�Բ��Բ��ΪP������B��x��Ĵ��ߣ�����ΪE�����ڰ�ԲP���ڵ�D��
��ͼ���ཻ�İ�Բ��Բ��ΪP������B��x��Ĵ��ߣ�����ΪE�����ڰ�ԲP���ڵ�D�� 
��1����m=5ʱ����B��C��������꣮
��2����֤������mȡ��ֵ���߶�DE�ij�ʼ��Ϊ��ֵ��
��3���ǵ�C����ֱ��DE�ĶԳƵ�ΪC�䣬���ı���CDC��EΪ����ʱ����m��ֵ��
���𰸡�
��1���⣺��m=5����y=��x+m�еã�y=��x+5��
��  ��ã�
��ã� ![]() ��
�� ![]() ��
��
��B��1��4����C��4��1����
��2���⣺��ͼ1������OD��AD��
��A��m��0����
��OA=m��
y=��x+m�У���x=0ʱ��y=m����F��0��m����
��OF=m��
���AOF�ǵ���ֱ�������Σ�
���OAB=45�㣬
��BE��OA��
���ABE�ǵ���ֱ�������Σ�
��BE=AE��
��OA�ǡ�P��ֱ����
���ODA=90�㣬
�ߡ�ODE=��OAD��
�ߡ�OED=��DEA=90�㣬
���ODE�ס�DAE��
�� ![]() ��
��
��DE2=OEAE=OEBE��
��B�Ƿ����������ϵĵ㣬��OEBE=4
������mȡ��ֵ���߶�DE�ij�ʼ��Ϊ��ֵ��
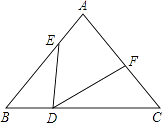
��3���⣺��ͼ3������CC�䣬��DE��CC�佻��G��

�ɣ�2���ã�DE2=4��
��DE=2��
���ı���CDC��EΪ���Σ�
��DG=EG=1��
��C��������Ϊ1��
��y=1ʱ�� ![]() =1��x=4��
=1��x=4��
��C��4��1����
��C��4��1������y=��x+m�еã���4+m=1��
m=5��
����������1����M=5����һ�κ�������ʽ�У��뷴���������з����������ɣ���2���������ߣ���ͼ1��֤����ODE�ס�DAE���б���ʽ�ã� ![]() ����DE2=OEAE=OEBE=4�������߶�DE�ij�ʼ��Ϊ��ֵ����3���������ε��������C�����꣬����һ�κ����Ľ���ʽ�пɵ�m��ֵ��
����DE2=OEAE=OEBE=4�������߶�DE�ij�ʼ��Ϊ��ֵ����3���������ε��������C�����꣬����һ�κ����Ľ���ʽ�пɵ�m��ֵ��

 ��ѧʵ����ϵ�д�
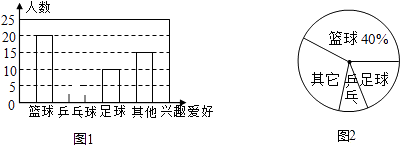
��ѧʵ����ϵ�д�����Ŀ�����ؿ�����ij���ӵ�·�峧������ɽ��ѧ��Ӧ���ҵ������Ƹ��˾ְԱ����ӦƸ�ߵ�רҵ֪ʶ��Ӣ��ˮƽ���μ����ʵ�������Ż��������в��Ի�ɹ��϶�������ĵ÷����ֶ�Ϊ100�֣�����ķ����ֱ�5��3��2�ı�������ÿ�˵�����ܷ֣���4λӦƸ�ߵĵ÷����±���ʾ��
| רҵ֪ʶ | Ӣ��ˮƽ | �μ����ʵ���� ���Ż�� |
�� | 85 | 85 | 90 |
�� | 85 | 85 | 70 |
�� | 80 | 90 | 70 |
�� | 90 | 90 | 50 |
��1���ֱ����4λӦƸ�ߵ��ܷ֣�
��2���������ˡ�רҵ֪ʶ����ƽ����Ϊ85�֣�����Ϊ12.5�����ˡ�Ӣ��ˮƽ����ƽ����Ϊ87.5�֣�����Ϊ6.25������������ˡ��μ����ʵ�������Ż�ȡ���ƽ���ּ����
��3��������1���ͣ�2���е��й����ݣ���Դ�ѧ��ӦƸ���кν��飿