题目内容
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
【答案】(1)一个球为白球,一个球为红球的概率是![]() ;
;
(2)该游戏规则不公平.
【解析】试题分析:(1)画树状图列出所有等可能结果数,再根据概率公式计算即可得;
(2)分别求出甲获胜和乙获胜的概率,比较后即可得.
试题解析:(1)画树状图如下:
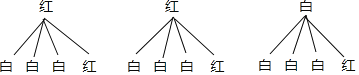
由树状图可知,共有12种等可能情形,其中一个球为白球,一个球为红球的有7种,
∴一个球为白球,一个球为红球的概率是![]() ;
;
(2)由(1)中树状图可知,P(甲获胜)=![]() ,P(乙获胜)=
,P(乙获胜)=![]() ,
,
∵![]() ,
,
∴该游戏规则不公平.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目