Question

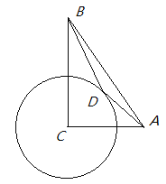
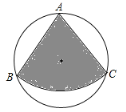
【题目】如图，从一块半径为的圆形铁皮上剪出一个圆心角是的扇形，则此扇形围成的圆锥的侧面积为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

连接OB、OC和BC，过点O作OD⊥BC于点D，然后根据同弧所对的圆周角是圆心角的一半、等边三角形判定和垂径定理可得∠BOC=2∠BAC=120°，△ABC为等边三角形，BC=2BD，然后根据锐角三角函数即可求出BD，从而求出BC和AB，然后根据扇形的面积公式计算即可．

解：连接OB、OC和BC，过点O作OD⊥BC于点D

由题意可得：OB=OC=20cm，∠BAC=60°，AB=AC

∴∠BOC=2∠BAC=120°，△ABC为等边三角形，BC=2BD

∴∠OBC=∠OCB=（180°－∠BOC）=30°，AB=AC=BC

在Rt△OBD中，BD=OB·cos∠OBD=cm

∴BC=2BD=cm

∴AB=BC=cm

∴圆锥的侧面积=S扇形BAC=

故选A．