Question

【题目】如图，⊙O是△ABC的外接圆，圆心O在AB上，M是OA上一点，过M作AB的垂线交BC的延长线于点E，过点C作⊙O的切线，交ME于点F．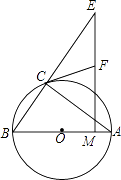

（1）求证：EF=CF；
（2）若∠B=2∠A，AB=4，且AC=CE，求BM的长．

Answer 1

【答案】
（1）证明：延长FC至H，如图所示：

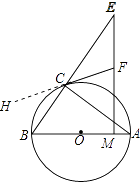
∵⊙O是△ABC的外接圆，圆心O在AB上，

∴AB是⊙O的直径，

∴∠ACB=90°，

∵EM⊥AB，

∴∠EMB=∠ACB=90°，

∵∠ABC=∠EBM，

∴△ABC∽△EMB，

∴∠CEF=∠CAB，

∵FC是⊙O的切线，

∴∠CAB=∠BCH，

∵∠BCH=∠ECF

∴∠CAB=∠ECF，

∴∠CEF=∠ECF，

∴EF=CF；

（2）解：∵∠ACB=90°，∠B=2∠A，

∴∠B=60°，∠A=30°，

在Rt△ABC中，∠ACB=90°，∠A=30°，AB=4，

∴BC= AB=2，AC= BC=2 ，

∵AC=CE，

∴CE=2 ，

∴BE=BC+CE=2+2 ，

在Rt△BEM中，∠BME=90°，∠BEM=∠A=30°

∴BM= BE=1+ ．

【解析】（1）延长FC至H，由AB是⊙O的直径，得出∠ACB=90°，由EM⊥AB，得出∠EMB=∠ACB=90°，证得△ABC∽△EMB，得出∠CEF=∠CAB，由弦切角定理得出∠CAB=∠BCH，由对顶角相等得出∠BCH=∠ECF，推出∠CEF=∠ECF，即可得出结论；（2）利用含30度的直角三角形三边的性质得出BC= AB=2，AC= BC=2 ，则CE=2 ，所以BE=BC+CE=2+2 ，然后在Rt△BEM中计算出BM= BE即可．
【考点精析】本题主要考查了三角形的外接圆与外心和切线的性质定理的相关知识点，需要掌握过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．