题目内容
如图,将长8 cm,宽4 cm的矩形纸片ABCD折叠,使点A与C重合,则折痕EF的长等于 Cm

2

分析:连接A、C,则EF垂直平分AC,推出△OEC∽△BCA,根据勾股定理,可以求出AC的长度,根据相似比求出OE即可.
解答:解:连接AC,与EF交于O点,

∵E点在AB上,F在CD上,因为A、C点重合,EF是折痕,
∴AO=CO,EF⊥AC,
∵AB=8,BC=4,
∴AC=4 ,
,
∵AE=CE,
∴∠EAO=∠ECO,
∴△OEC∽△BCA,
∴OE:BC=OC:BA,
∴OE= ,
,
∴EF=2OE=2 .
.
故答案为:2 .
.
解答:解:连接AC,与EF交于O点,

∵E点在AB上,F在CD上,因为A、C点重合,EF是折痕,
∴AO=CO,EF⊥AC,
∵AB=8,BC=4,
∴AC=4
 ,
,∵AE=CE,
∴∠EAO=∠ECO,
∴△OEC∽△BCA,
∴OE:BC=OC:BA,
∴OE=
 ,
,∴EF=2OE=2
 .
.故答案为:2
 .
.
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目



 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 处,
处,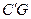 与
与 与
与 于点M、N.若点
于点M、N.若点 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.




 ,若重叠四边形
,若重叠四边形