题目内容
如图，在梯形ABCD中，AD∥BC，AB=DC，AC⊥BD于点O，过点A作AE⊥BC于点E，若BC=2AD=8，则tan∠ABE=__________。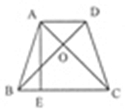
3
过D点作DF∥AC交BC的延长线于点F，构造等腰直角三角形后求得AE的长和BE的长，利用锐角三角函数的定义求解即可．
解：过D点作DF∥AC交BC的延长线于点F，
∵AC⊥BD于点O，
∴BD⊥FD，
∵AD∥BC，
∴AD=CF，
∴BF=BC+CF=8+4=12，
∵AC=BD，
∴BD=DF，
∴AC=BD=12÷
=6，
∴AE=
=6，
∴tan∠ABE=
=
=3．
故答案为：3．
本题考查了等腰三角形的性质，解题的关键是正确的平移梯形的对角线．
解：过D点作DF∥AC交BC的延长线于点F，
∵AC⊥BD于点O，
∴BD⊥FD，
∵AD∥BC，
∴AD=CF，
∴BF=BC+CF=8+4=12，
∵AC=BD，
∴BD=DF，
∴AC=BD=12÷
=6，∴AE=
=6，∴tan∠ABE=
==3．故答案为：3．
本题考查了等腰三角形的性质，解题的关键是正确的平移梯形的对角线．
练习册系列答案
相关题目
；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（ ）
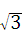，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．
中，
，
平分
，
交
于
.
是菱形；
的形状，并说明理由.
.
?若存在，请求出该点坐标，若不存在，请说明理由.