题目内容
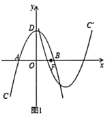
【题目】如图1.在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,顶点为
两点,顶点为![]() ,设点
,设点![]() 是
是![]() 轴的正半轴上一点,将抛物线
轴的正半轴上一点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
![]() 求抛物线
求抛物线![]() 的函数表达式:
的函数表达式:
![]() 若抛物线
若抛物线![]() 与抛物线
与抛物线![]() 在
在![]() 轴的右侧有两个不同的公共点,求
轴的右侧有两个不同的公共点,求![]() 的取值范围.
的取值范围.
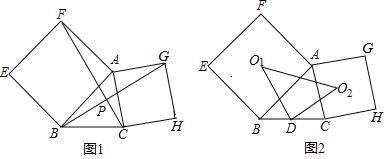
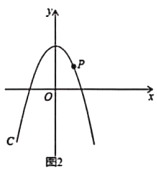
![]() 如图2,
如图2,![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,它到两坐标轴的距离相等,点
上一点,它到两坐标轴的距离相等,点![]() 在抛物线
在抛物线![]() 上的对应点
上的对应点![]() ,设
,设![]() 是
是![]() 上的动点,
上的动点,![]() 是
是![]() 上的动点,试探究四边形
上的动点,试探究四边形![]() 能否成为正方形?若能,求出
能否成为正方形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】![]()
![]() ;
;![]()
![]() ;
;![]() 四边形
四边形![]() 可以为正方形,
可以为正方形,![]()
【解析】
(1)由题意得出A,B坐标,并代入![]() 坐标利用待定系数法求出抛物线
坐标利用待定系数法求出抛物线![]() 的函数表达式;
的函数表达式;
(2)根据题意分别求出当![]() 过点
过点![]() 时m的值以及当
时m的值以及当![]() 过点
过点![]() 时m的值,并以此进行分析求得;
时m的值,并以此进行分析求得;
(3)由题意设![]() ,代入解出n,并作
,代入解出n,并作![]() ,
,![]() 于
于![]() ,利用正方形性质以及全等三角形性质得出M为
,利用正方形性质以及全等三角形性质得出M为![]() ,将
,将![]() 代入
代入![]() 即可求得答案.
即可求得答案.
解:![]()
![]()
![]()
将![]() 三点代入得
三点代入得![]()
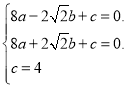 解得
解得
![]() ;
;
![]() 如图
如图![]() .
.

关于![]() 对称的抛物线为
对称的抛物线为
![]()
当![]() 过点
过点![]() 时有
时有![]()
解得:![]()
当![]() 过点
过点![]() 时有
时有![]()
解得:![]()
![]() ;
;
![]() 四边形
四边形![]() 可以为正方形
可以为正方形
由题意设![]() ,
,
![]() 是抛物线
是抛物线![]() 第一象限上的点
第一象限上的点
![]()
解得:![]() (舍去)即
(舍去)即![]()
如图作![]() ,
,![]() 于
于![]() ,
,
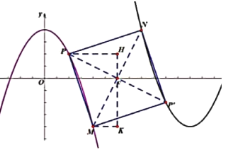
![]() 于
于![]()
![]() 四边形
四边形![]() 为正方形
为正方形
易证![]()
![]()
![]()
![]() 为
为![]()
![]() 将
将![]() 代入
代入![]() 得
得
![]()
解得:![]() (舍去)
(舍去)
![]() 当
当![]() 时四边形
时四边形![]() 为正方形.
为正方形.

练习册系列答案
相关题目