��Ŀ����
����Ŀ����ͼ��A(0��2)��B(6��2)��C(0��c)(c��0)����AΪԲ��AB��Ϊ�뾶��![]() ��y���������ڵ�D��
��y���������ڵ�D��![]() ��BC�н���ʱ������ΪE��PΪ
��BC�н���ʱ������ΪE��PΪ![]() ��һ�㣮
��һ�㣮
(1)��c��6![]() +2��
+2��
��BC��_____��![]() �ij�Ϊ_____��
�ij�Ϊ_____��
�ڵ�CP��6![]() ʱ���ж�CP���A��λ�ù�ϵ��������֤����
ʱ���ж�CP���A��λ�ù�ϵ��������֤����
(2)��c��10�����P��BC��������ֵ��
(3)�ֱ�ֱ��д����c��1��c��6��c��9��c��11ʱ����P��BC��������(������軯��)

���𰸡�(1)��12��������CP���A���У�(2)��c��10����P��BC��������ֵ��![]() ��(3)c=1ʱ��PM=
��(3)c=1ʱ��PM=![]() ��c=6ʱ��PF��6��
��c=6ʱ��PF��6��![]() ��c=9ʱ��PF��6��
��c=9ʱ��PF��6��![]() ��c=11ʱ��PG��
��c=11ʱ��PG��![]() .
.
��������
(1)�������AB��AC���������BC�͡�ABC������û�����ʽ���ɵó����ۣ����жϳ���APC��ֱ�������Σ����ɵó����ۣ�
(2)��������������������ε������������Ǻ������ɵó����ۣ�
(3)��ͼͼ�Σ�ͬ(2)�ķ������ɵó����ۣ�
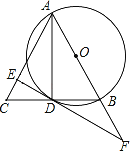
�⣺(1)����ͼ1������AE��
��c��6![]() +2��
+2��
��OC��6![]() +2��
+2��
��AC��6![]() +2��2��6
+2��2��6![]() ����AB��6��
����AB��6��
��Rt��BAC�У����ݹ��ɶ����ã�BC��12��tan��ABC��![]() ��
��![]() ��
��
���ABC��60����
��AE��AB��
���ABE�ǵȱ������Σ�
���BAE��60����
���DAE��30����
��![]() �ij�Ϊ
�ij�Ϊ![]() ������
������
�ʴ�Ϊ12������

��CP���A����
֤������AP��AB��6��AC��OC��OA��6![]() ��
��
��AP2+CP2��108��
��AC2��(6![]() )2��108��
)2��108��
��AP2+PC2��AC2��
���APC��90��������CP��AP��
��AP�ǰ뾶��
��CP���A����
(2)��c��10����AC��10��2��8����BC��10��
������P��![]() �ϣ�AP��BEʱ����P��BC�ľ�������费��ΪF��
�ϣ�AP��BEʱ����P��BC�ľ�������费��ΪF��
��PF�ij����������룬��ͼ2��
S��ABC��![]() AB��AC��
AB��AC��![]() BC��AF��
BC��AF��
��AF��![]() ��
��![]() ��
��
��PF��AP��AF��![]()

����ͼ3������P��![]() �ϣ���PG��BC�ڵ�G��
�ϣ���PG��BC�ڵ�G��
����P���D�غ�ʱ��PG���
��ʱ��sin��ACB��![]() ��
��
��PG��![]() ��
��![]() ��
��
����c��10����P��BC��������ֵ��![]() ��
��

(3)��c��1ʱ����ͼ4

����P��PM��BC��sin��BCP��![]()
��PM��![]() ��
��![]() ��
��
��c��6ʱ����ͼ5��ͬc��10�Ģ������PF��6��![]() ��
��

��c��9ʱ����ͼ6��ͬc��10�Ģ������PF��6��![]() ��
��

��c��11ʱ����ͼ7��

��P�͵�D�غ�ʱ����P��BC�ľ������ͬc��10ʱ�������PG��![]() ��
��

 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�����Ŀ��ij����������ij����5000����Ϊ�˹��Ƹ������и���������������������в�����3�Σ�ȡ�õ��������£�
����/�� | ƽ��ÿ���������/kg | |
��1��� | 20 | 1.6 |
��2��� | 15 | 2.0 |
��3��� | 15 | 1.8 |
��1����������ƽ��ÿ�����������
��2������������������������
��3���������ÿǧ�˵��ۼ�Ϊ14Ԫ������۸����������y��Ԫ������۸����������x��kg��֮��ĺ�����ϵ���������Ա���x��ȡֵ��Χ��