题目内容
【题目】在每个小正方形的边长为![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换.例如,在
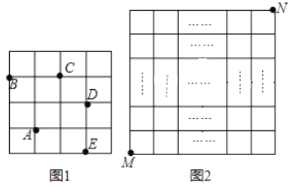
的另一个格点的运动称为一次跳马变换.例如,在![]() 的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点![]() 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点![]() ,
,![]() ,
,![]() ,
,![]() 等处现有
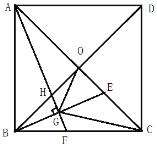
等处现有![]() 的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点![]() 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点![]() ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据题意画出F点,由图一计算出规律即可推出.
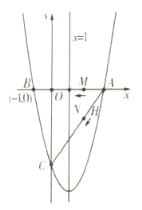
如图1,连接AC,CF,则AF=![]() ,
,
∴两次变换相当于向右移动3格,向上移动3格.
又∵MN=![]() ,∴
,∴![]() (不是整数),
(不是整数),
∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处.
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是14次.
故选D.

 同步轻松练习系列答案
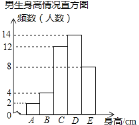
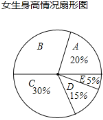
同步轻松练习系列答案【题目】某校为了了解学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成下面的统计图表:
组别 | A | B | C | D | E |
身高(cm) | x<150 | 150≤x<155 | 155≤x<160 | 160≤x<165 | x≥165 |
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
(3)从男生样本的A、B两组里,随机安排2人参加一项活动,求恰好是1人在A组、1人在B组的概率.
【题目】生物学上研究表明:不同浓度的生长素对植物的生长速度影响不同,在一定范围内,生长素的浓度对植物的生长速度有促进作用,相反,在某些浓度范围,生长速度会变缓慢,甚至阻碍植物生长(阻碍即植物不生长,甚至枯萎).小林同学在了解到这一信息后,决定研究生长素浓度与茶树生长速度的关系,设生长素浓度为x克/升,生长速度为y毫米/天,当x超过4时,茶树的生长速度y与生长素x浓度满足关系式:![]() .实验数据如下表,当生长速度为0时,实验结束.
.实验数据如下表,当生长速度为0时,实验结束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如图,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,画出该函数图象;
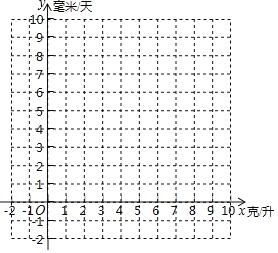
(2)根据上述表格,求出整个实验过程中y与x的函数关系式,并写出自变量x的取值范围;
(3)结合画出的函数图象,写出该函数的一条性质: ;
(4)若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是: .