题目内容
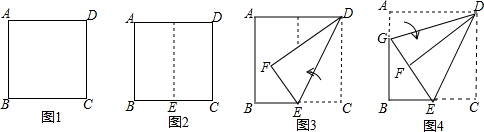
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,
(1)求BF的长;
(2)求折痕AE的长.

(1)求BF的长;
(2)求折痕AE的长.

(1)由题意可得:△AEF≌△AED
∴AF=AD,
∴∠ABF=90°
∴在△ABF中,由勾股定理得BF=6cm;
(2)设DE长x,则EF也长x,
EC长8-x.
由(1)得:CF=BC-BF=4.
在△CEF中,由勾股定理CE2+CF2=EF2
列方程得:(8-x)2+42=x2
解得x=5cm.
再在△ADE中,由勾股定理解得AE=
=
=5
cm.

∴AF=AD,
∴∠ABF=90°
∴在△ABF中,由勾股定理得BF=6cm;
(2)设DE长x,则EF也长x,
EC长8-x.
由(1)得:CF=BC-BF=4.
在△CEF中,由勾股定理CE2+CF2=EF2
列方程得:(8-x)2+42=x2
解得x=5cm.
再在△ADE中,由勾股定理解得AE=
| AD2+DE2 |
| 125 |
| 5 |


练习册系列答案
相关题目