题目内容
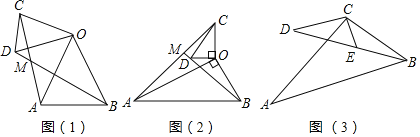
【题目】(感知)如图①,正方形![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() 平分
平分![]() .若我们分别延长
.若我们分别延长![]() 与
与![]() ,交于点
,交于点![]() ,则易证
,则易证![]() .(不需要证明)
.(不需要证明)
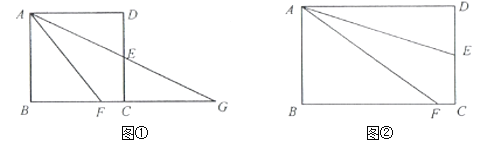
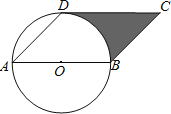
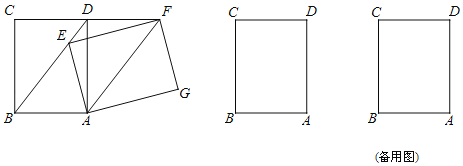
(探究)如图②,在矩形![]() 中,点
中,点![]() 在
在![]() 边的中点,点
边的中点,点![]() 在
在![]() 边上,
边上,![]() 平分
平分![]() .求证:
.求证:![]() .
.
(应用)在(探究)的条件下,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】【感知】见解析;【探究】见解析;【应用】![]()
【解析】
感知:如图①,根据平行线的性质和角平分线的定义可得出结论;
探究:如题②,作辅助线,证明△AED≌△GEC,得到AD=CG=BC,再由感知中得到AF=FG,可得出结论;
应用:设FC=x,则AF=x+6,BF=6-x,由勾股定理列方程可得结论.
感知:
证明:如图①
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠G,
∵AE平分∠DAF,
∴∠DAE=∠FAG,
∴∠FAG=∠G,
∴AF=FG.
探究:
解:如图,分别延长![]() 与
与![]() ,交于点
,交于点![]() .
.
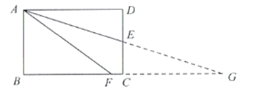
∵点E是CD边的中点,
∴DE=EC.
![]() 矩形
矩形![]() ,
,
![]()
![]() ,
,
![]() ,
,
又![]() ,
,
![]() (ASA),
(ASA),
![]() ,
,![]() ,
,
![]() 是
是![]() 的平分线,
的平分线,
![]() ,
,
![]() .
.
即![]() .
.
应用:
解:如图②,设FC=x,则AF=x+6,BF=6-x,
∵点E是DC的中点,DE=2,
∴DC=4,
在Rt△ABF中,由勾股定理得:AF2=AB2+BF2,
(6+x)2=42+(6-x)2
解得:![]() ,
,
∴![]() .
.

练习册系列答案
相关题目