题目内容
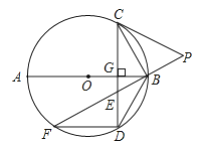
【题目】如图,已知AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
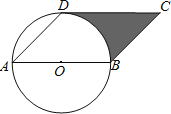
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的周长.
【答案】(1)直线CD与⊙O相切,理由见解析;(2)2+![]() +
+![]()
【解析】
(1)直线与圆的位置关系无非是相切或不相切,可连接OD,证OD是否与CD垂直即可.
(2)阴影部分的周长可由CD+BC+扇形OBD的弧长求得;扇形的半径和圆心角已求得,那么关键是求出平行四边形CD的长,可通过证四边形ABCD是平行四边形,得出CD=AB,由此可求出CD的长,即可得解.
解:(1)直线CD与⊙O相切.理由如下:
如图,连接OD,
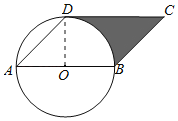
∵OA=OD,∠DAB=45°,
∴∠ODA=45°,
∴∠AOD=90°,
∵CD∥AB,
∴∠ODC=∠AOD=90°,即OD⊥CD,
又∵点D在⊙O上,
∴直线CD与⊙O相切;
(2)∵⊙O的半径为1,AB是⊙O的直径,
∴AB=2,
∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2,
由(1)知:△AOD是等腰直角三角形,
∵OA=OD=1,
∴BC=AD=![]() ,
,
∴图中阴影部分的周长=CD+BC+![]() =2+
=2+![]() +
+![]() .
.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目