��Ŀ����
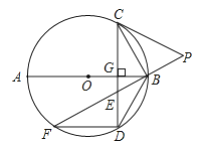
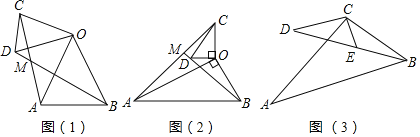
����Ŀ�����������֣���ͼ��1�����ڡ�OAB�͡�OCD�У�OA��OB��OC��OD����AOB����COD��45�㣬����AC��BD���ڵ�M��
��AC��BD֮���������ϵΪ�� ����
����AMB�Ķ���Ϊ�� ����
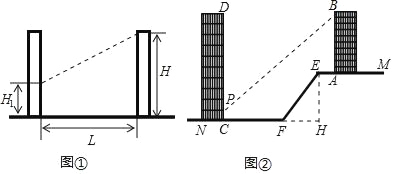
�����̽������ͼ��2�����ڡ�OAB�͡�OCD�У���AOB����COD��90�㣬��OAB����OCD��30�㣬����AC����BD���ӳ����ڵ�M�������![]() ��ֵ����AMB�Ķ�����
��ֵ����AMB�Ķ�����
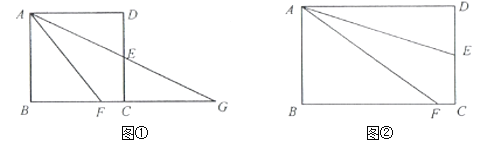
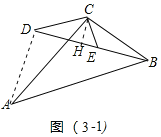
��ʵ��Ӧ�ã���ͼ��3������һ��������������30��ǵĴ�С��ͬ��ֱ�����ǰ�ABC��DCE��ɵ�ͼ�Σ����С�ACB����DCE��90�㣬��A����D��30����D��E��B��ͬһֱ���ϣ�CE��1��BC��![]() �����A��D֮��ľ��룮
�����A��D֮��ľ��룮
���𰸡����������֡���AC=BD������AMB=45�㣻�����̽����![]() ����AMB=90�㣻��ʵ��Ӧ�á�4
����AMB=90�㣻��ʵ��Ӧ�á�4![]() ��5
��5![]()
��������
��������:��ͼ��1����֤����COA�ա�DOB��SAS�������ɽ�����⣮
���̽��:��ͼ��2����֤����COA�ס�ODB���ɵ�![]() ����MAK����OBK���ѽ���ɽ�����⣮
����MAK����OBK���ѽ���ɽ�����⣮
ʵ��Ӧ��:���������ν�ֱ�����������BE�����������������ε����ʽ�����⼴�ɣ�
�⣺��������:��ͼ��1���У���OA��BD��K��
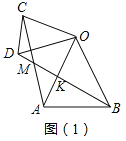
�ߡ�AOB����COD��45����
���COA����DOB��
��OA��OB��OC��OD��
���COA�ա�DOB��SAS����
��AC��DB����CAO����DBO��
�ߡ�MKA����BKO��
���AMK����BOK��45����
�ʴ�Ϊ��AC��BD����AMB��45��
���̽��:��ͼ��2���У�
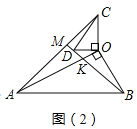
����OAB����OCD�У��ߡ�AOB����COD��90������OAB����OCD��30����
���COA����DOB��OC��![]() OD��OA��
OD��OA��![]() OB��
OB��
��![]() ��
��
���COA�ס�ODB��
��![]() ����MAK����OBK��
����MAK����OBK��
�ߡ�AKM����BKO��
���AMK����BOK��90����
ʵ��Ӧ��:��ͼ3��1�У���CH��BD��H������AD��
��Rt��DCE�У��ߡ�DCE��90������CDE��30����EC��1��
���CEH��60����
�ߡ�CHE��90����
���HCE��30����
��EH��![]() EC��
EC��![]() ��
��
��CH��![]() ��
��
��Rt��BCH��BH��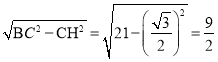 ��
��
��BE��BH��EH��4��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��4![]() ��
��
��ͼ3��2�У�����AD���� CH��DE��H��
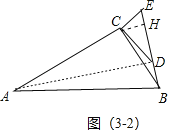
ͬ���ɵ�BH��![]() ��EH��
��EH��![]() ��
��
��BE��![]() +
+![]() ��5��
��5��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��5![]() ��
��

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�����Ŀ��ij�̳�ͬʱ�����ס���������Ʒ��100��������ۺ��ۼ����±���
��Ʒ���� | �� | �� |
����(Ԫ/��) | 40 | 90 |
�ۼ�(Ԫ/��) | 60 | 120 |
�����м�����Ʒ����x�����̳�������100����Ʒ��������ΪyԪ��
(��)д��y����x�ĺ�����ϵʽ��
(��)���̳��ƻ����Ͷ��8000Ԫ���ڹ�����������Ʒ��
������Ҫ�������ټ�����Ʒ��
������������Щ��Ʒ�����̳��ɻ�õ���������Ƕ���Ԫ��