��Ŀ����
����Ŀ����ͼ�����κ���![]() ��ͼ��
��ͼ��![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ�ö��κ���ͼ�㣮����
Ϊ�ö��κ���ͼ�㣮����![]() ��
��![]() ��
��![]() ��
��![]() ��
��


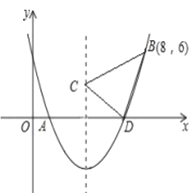
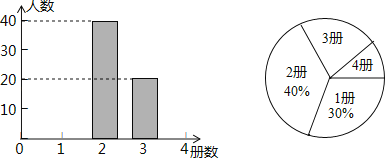
��1����ͼ1������![]() ������
������![]() ������
������![]() ����
����![]() ��
��
����![]() ��ֵ����˵��
��ֵ����˵��![]() ��
��
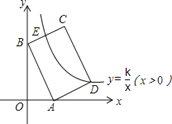
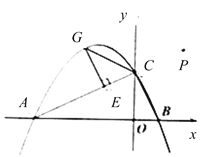
����ͼ2����![]() �������ߵĶԳ�����һ�㣬�Ե�
�������ߵĶԳ�����һ�㣬�Ե�![]() ΪԲ�ĵ�Բ����
ΪԲ�ĵ�Բ����![]() ��
��![]() ���㣬����ֱ��
���㣬����ֱ��![]() ���У����
���У����![]() �����ꣻ
�����ꣻ
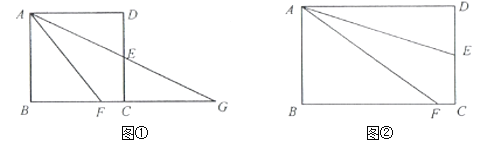
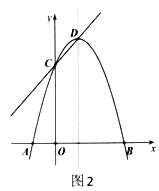
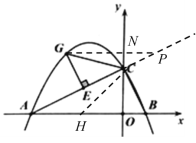
��2����![]() ����
����![]() ����
����![]() ����ͼ3������
����ͼ3������![]() ��ֱ��
��ֱ��![]() �Ϸ��Ķ��κ���ͼ���ϣ�����
�Ϸ��Ķ��κ���ͼ���ϣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �е�ij����ǡ�õ���
�е�ij����ǡ�õ���![]() ��2���������ڣ������
��2���������ڣ������![]() �ĺ����꣺�������ڣ���˵�����ɣ�
�ĺ����꣺�������ڣ���˵�����ɣ�
���𰸡���1����![]() �����������ڵ�P������Ϊ��1����4+
�����������ڵ�P������Ϊ��1����4+![]() ����1����4��
����1����4��![]() ������2��G�����
������2��G�����![]() ��
��![]()
��������
��1������![]() ������B������룬���aֵ���õ������߱���ʽ����y=0�������A���꣬����OB��OC�ó���CBO=��OCB���ٸ��ݸ����������BC��DC��BD�ij���֤����BCD��ֱ�������Σ��Ƴ���DBC=��OCA���Ӷ��õ����ۣ�
������B������룬���aֵ���õ������߱���ʽ����y=0�������A���꣬����OB��OC�ó���CBO=��OCB���ٸ��ݸ����������BC��DC��BD�ij���֤����BCD��ֱ�������Σ��Ƴ���DBC=��OCA���Ӷ��õ����ۣ�
����ֱ��CD�С�P�ڵ�E������PE��PA����CF��DQ�ڵ�F��֤����DEPΪ���������Σ���P��1��m�����ڡ�APQ�У����ù��ɶ����г����̣����m���ɵõ�P���ꣻ
��2����![]() ��
��![]() ��������ֱ����ۣ��г���Ӧ���̣���֮����.
��������ֱ����ۣ��г���Ӧ���̣���֮����.
�⣺��1������![]() ����B��3��0�����룬
����B��3��0�����룬
���![]() ��
��
�������ߵĽ���ʽ�ǣ�![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��A����1��0����
��![]() ��
��
���CBO=��OCB��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��ֱ����������
��ֱ����������![]() ��
��
��![]() ��
��
�֡ߡ�DBC�͡�OCA������ǣ�
���DBC=��OCA��
���DBA=��ACB��
����ͼ����ֱ��CD�С�P�ڵ�E������PE��PA����CF��DQ�ڵ�F��
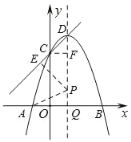
��PE��CD��PE=PA��
��y=��x2+2x+3���ã��Գ���Ϊֱ��x=1��C��0��3����D��1��4����
��DF=4��3=1��CF=1��
��DF=CF��
���DCFΪ����ֱ�������Σ�
���CDF=45����
���EDP=��EPD=45����
��DE=EP��
���DEP����������
��P��1��m����D��1��4����
��![]() ��
��
��![]() ��
��
��EP2=![]() ��4��m��2��
��4��m��2��
�ڡ�APQ�У���PQA=90����
��AP2=AQ2+PQ2=[1-��-1��]2+m2
��![]() ��4��m��2=[1-��-1��]2+m2��
��4��m��2=[1-��-1��]2+m2��
��������m2+8m��8=0��
��ã�m=��4��![]() ��
��
���P��������1����4+![]() ����1����4��
����1����4��![]() ����
����
��2��G�����![]() ��
��![]() ��
��
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
��![]() ��
��
���ǣ�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ���ᣩ��
���ᣩ��![]() ��
��
��![]() ��
��
����![]() ��
��
ȡ![]() ���е�
���е�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
�� ��
��
��![]() ��
��
��![]()
�ʵ�G�ĺ�����![]() ��
��![]() .
.