Question

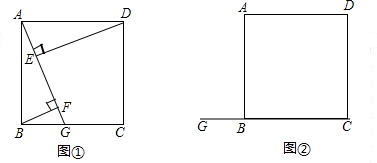
如图，正方形ABCD的边长为2

2

，E是边AD上的一个动点（不与A重合），BE交对角线于F，连接
DF．
（1）求证：BF=DF；
（2）设AF=x，△ABF面积为y，求y与x的函数关系式，并画出图象．

Answer 1

（1）证明：∵四边形ABCD为正方形，
∴∠BAC=∠DAC=45°，AB=AD，
在△ABF和△ADF中，
∵

AB=AD ∠BAC=∠DA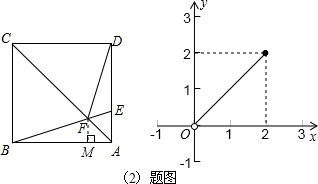C AF=AF

，
∴△ABF≌△ADF（SAS），
∴BF=DF；

（2）如图，过点F作FM⊥AB，
∵∠BAC=45°（正方形的对角线平分一组对角），
∴FM=

2

2

AF=

2

2

x，
∴y=

1

2

AB•FM=

1

2

×2

2

×

2

2

x=x，
∵E是边AD上的一个动点，
∴AF的最大值为

1

2

AC=

1

2

×

2

AB=

1

2

×

2

×2

2

=2，
∴自变量的取值范围是0＜x≤2，
故y与x的函数关系式为y=x（0＜x≤2），图象如图．