题目内容

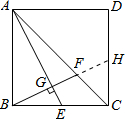
如图，正方形ABCD的边长为2，点E是BC边的中点，过点B作BG⊥AE，垂足为G，延长BG交AC于点F，则CF=______．
延长BF交CD于H．
在正方形ABCD中，正方形的边长是2，根据勾股定理，得AC=2
2
．
∵AB=BC，∠ABE=∠BCH=90°，∠BAE=∠CBH，
∴△ABE≌△BCH，
∴CH=BE=1．
∵AB∥CD，
∴△ABF∽△CHF，
∴
AF
CF
=
AB
CH
=2，
∴CF=
1
3
AC=
2
2
3
．
故答案为
2
2
3
．
练习册系列答案
相关题目
已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．
（1）当∠MAN绕点A旋转到BM=DN时（如图1），求证：BM+DN=MN；
（2）当∠MAN绕点A旋转到BM≠DN时（如图2），则线段BM，DN和MN之间数量关系是______；
（3）当∠MAN绕点A旋转到如图3的位置时，猜想线段BM，DN和MN之间又有怎样的数量关系呢？并对你的猜想加以说明．
（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．
（1）如图（1），点M，N分别在等边△ABC的BC，AC边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．
（2）判断下列命题的真假性：
①若将题（1）中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？
②若将题（1）中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°？（如图2）
③若将题（1）中的条件“点M，N分别在正△ABC的BC，AC边上”改为“点M，N分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM=60°？（如图3）
在下列横线上填写“是”或“否”：①______；②______；③______．并对②，③的判断，选择其中的一个给出证明．
如图，EF与MN将正方形ABCD恰好分成两个矩形和两小正方形，如果AB=1，则正方形AMPE与正方形PFCN的周长和为______．
如图，正方形ABCD的边长为2
2
，E是边AD上的一个动点（不与A重合），BE交对角线于F，连接
DF．
（1）求证：BF=DF；
（2）设AF=x，△ABF面积为y，求y与x的函数关系式，并画出图象．
如图所示，正方形ABCD的边长为1，点E为AB的中点，以E为圆心，1为半径作圆，分别交AD，BC于M，N两点，与DC切于点P，则图中阴影部分面积是______．
如图，E为正方形ABCD内的一点，△ABE为正三角形，求∠CED的度数．
操作示例：
对于边长为a的两个正方形ABCD和EFGH，按图1所示的方式摆放，在沿虚线BD，EG剪开后，可以按图中所示的移动方式拼接为图1中的四边形BNED．
从拼接的过程容易得到结论：
①四边形BNED是正方形；
②S正方形ABCD+S正方形EFGH=S正方形BNED．
实践与探究：
（1）对于边长分别为a，b（a＞b）的两个正方形ABCD和EFGH，按图2所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N；
①证明四边形MNED是正方形，并用含a，b的代数式表示正方形MNED的面积；
②在图2中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简略说明你的拼接方法（类比图1，用数字表示对应的图形）；
（2）对于n（n是大于2的自然数）个任意的正方形，能否通过若干次拼接，将其拼接成为一个正方形？请简要说明你的理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网