题目内容
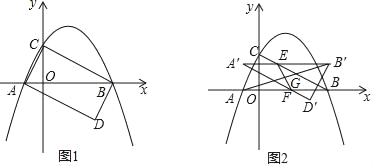
【题目】如图,ABCD位于直角坐标系中,AB=2,点D(0,1),以点C为顶点的抛物线y=ax2+bx+c经过x轴正半轴上的点A,B,CE⊥x轴于点E.
(1)求点A,B,C的坐标.
(2)将该抛物线向上平移m个单位恰好经过点D,且这时新抛物线交x轴于点M,N.
①求MN的长.
②点P是新抛物线对称轴上一动点,将线段AP绕点A顺时针旋转60°得AQ,则OQ的最小值为 (直接写出答案即可)
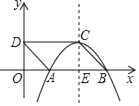
【答案】(1)A(1,0),B(3,0),C(2,1);(2)①MN=![]() ;②
;② ![]()
【解析】
(1)由ABCD可知CD,进而求出E和C点坐标,由AB长从而求出AB点.(2)①由第一问解出抛物线方程,上移m更改抛物线方程,由其过D,进而求出上移后抛物线方程,再求MN.②根据三角函数,求出最小值.
(1)∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵CE⊥x轴,
∴OE=2,
∵点E是AB中点,
∴AE=BE=1,
∴OA=2﹣1=1.OB=OE+BE=3,
∴A(1,0),B(3,0),
∵D(0,1),
∴C(2,1);
(2)由(1)知,抛物线的顶点C(2,1),
∴设抛物线的解析式为y=a(x﹣2)2+1,
∵A(1,0)在抛物线上,
∴a(1﹣2)2+1=0,
∴a=﹣1,
∴抛物线解析式为y=﹣(x﹣2)2+1,
①该抛物线向上平移m个单位恰好经过点D,设平移后的抛物线解析式为y=﹣(x﹣2)2+1+m,
∵D(0,1),
∴﹣(﹣2)2+1+m=1,
∴m=4,
∴平移后的抛物线解析式为y=﹣(x﹣2)2+5,
令y=0,
∴0=﹣(x﹣2)2+5,
∴x=2±![]() ,
,
∴M(2+![]() ,0),N(2﹣
,0),N(2﹣![]() ,0),
,0),
∴MN=2![]() ;
;
②如图,
在第一象限的抛物线对称轴上取一点P1,使∠P1AB=60°,
在Rt△AEP1中,AP1=2AE=2,P2E=![]()
∴点Q1和点B重合,
∴Q1(3,0),P1(2,![]() ),
),
在第一象限的抛物线对称轴上取一点P2,使∠P2AB=30°,
在Rt△AEP2中,P2E=AEtan30°=![]() ,
,
∴点Q2(2,﹣![]() ),
),
∴直线Q1Q2的解析式y=![]() x﹣
x﹣![]()
在第二象限的抛物线对称轴上取一点P3,使∠P3AE=60°,
由旋转知,Q3和点P1关于点A对称,
∴Q3(0,﹣![]() ),
),
∴点Q3在直线Q1Q2上,
∴点Q的运动轨迹是直线Q1Q2,
∴当OQ⊥Q1Q2时,OD最短,
∵Q1Q3=2![]()
∴OD最小=![]() =
=![]() ,
,
故答案为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案