题目内容
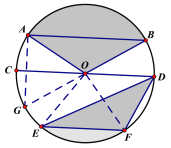
【题目】如图,CD是⊙O的直径,AB,EF是⊙O的弦,且AB∥CD∥EF,AB=16,CD=20,EF=12,则图中阴影部分的面积是( )
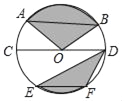
A. 96+25π B. 88+50π C. 50π D. 25π
【答案】C
【解析】
延长BO交⊙O于G,则BG是⊙O的直径,连接AG,根据圆周角定理得到∠GAB=90![]() ,根据勾股定理得到AG=12,求得AG=EF,推出S扇形AOG=S扇形EOF,根据已知条件可知S扇形EOF=S阴影DEF,于是得到阴影部分面积是⊙O面积的一半.
,根据勾股定理得到AG=12,求得AG=EF,推出S扇形AOG=S扇形EOF,根据已知条件可知S扇形EOF=S阴影DEF,于是得到阴影部分面积是⊙O面积的一半.
解:延长BO交⊙O于G,则BG是⊙O的直径,连接AG、OE、OF,
∴∠GAB=90,
∵AB=16,BG=CD=20,
∴AG=![]() ,
,
∴AG=EF,
∴![]() ,
,
∴S扇形AOG=S扇形EOF,
∵CD∥EF,
∴S△OEF=S△DEF,
∴S扇形EOF=S阴影DEF,
∴S扇形AOG= S阴影DEF,
∴S阴影=![]() S⊙O=
S⊙O=![]() =50
=50![]() .
.
故选C.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要![]() 元,一名小学生的学习费用需要
元,一名小学生的学习费用需要![]() 元.某校学生积极捐助,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
元.某校学生积极捐助,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
年级 | 捐款数额(元) | 捐助贫困中学生人数(名) | 捐助贫困小学生人数(名) |
初一年级 | 4000 | 2 | 4 |
初二年级 | 4200 | 3 | 3 |
初三年级 | 7400 |
(1)求![]() 的值;
的值;
(2)初三年级学生的捐款解决了其余贫困中小学生的学习费用,请将初三年级学生可捐助的贫困中、小学生人数直接填入表中.(不需写出计算过程).