题目内容
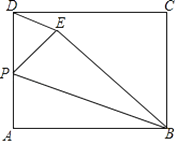
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
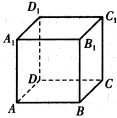
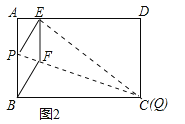
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

【答案】(1)证明见解析;(2)①菱形BFEP的边长为![]() cm;②点E在边AD上移动的最大距离为2cm.
cm;②点E在边AD上移动的最大距离为2cm.
【解析】试题分析:(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,因此BP=BF=EF=EP,即可得出结论;
(2)①由矩形的性质得出BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,由对称的性质得出CE=BC=5cm,在Rt△CDE中,由勾股定理求出DE=4cm,得出AE=AD﹣DE=1cm;在Rt△APE中,由勾股定理得出方程,解方程得出EP=![]() cm即可;
cm即可;
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
试题解析:解:(1)∵折叠纸片使B点落在边AD上的E处,折痕为PQ,∴点B与点E关于PQ对称,∴PB=PE,BF=EF,∠BPF=∠EPF.又∵EF∥AB,∴∠BPF=∠EFP,∴∠EPF=∠EFP,∴EP=EF,∴BP=BF=EF=EP,∴四边形BFEP为菱形;
(2)①∵四边形ABCD是矩形,∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°.∵点B与点E关于PQ对称,∴CE=BC=5cm.在Rt△CDE中,DE=![]() =4cm,∴AE=AD﹣DE=5cm﹣4cm=1cm.
=4cm,∴AE=AD﹣DE=5cm﹣4cm=1cm.
在Rt△APE中,AE=1,AP=3﹣PB=3﹣PE,∴EP2=12+(3﹣EP)2,解得:EP=![]() cm,∴菱形BFEP的边长为
cm,∴菱形BFEP的边长为![]() cm;
cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
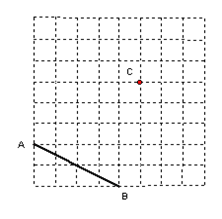
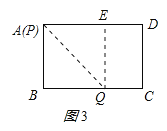
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,∴点E在边AD上移动的最大距离为2cm.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案