题目内容
【题目】在平面直角坐标系xOy中,函数![]() (
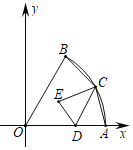
(![]() )的图象经过边长为2的正方形OABC的顶点B,如图,直线
)的图象经过边长为2的正方形OABC的顶点B,如图,直线![]() 与
与![]() (
(![]() )的图象交于点D(点D在直线BC的上方),与x轴交于点E .
)的图象交于点D(点D在直线BC的上方),与x轴交于点E .
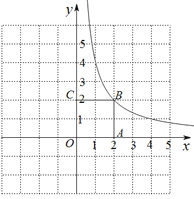
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记![]() (
(![]() )的图象在点B,D之间的部分与线段AB,AE,DE围成的区域(不含边界)为W.
)的图象在点B,D之间的部分与线段AB,AE,DE围成的区域(不含边界)为W.
①当![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有3个整点,结合函数图象,求m的取值范围.
【答案】(1)k=4;(2)①2个;②![]() .
.
【解析】
(1)把B点坐标代入函数y=![]() (x>0)中便可求得k的值;
(x>0)中便可求得k的值;
(2)①由m=![]() ,得出直线y=mx+m+1的解析式,画出图象,再根据定义求出区域W的整点个数便可;②当直线y=mx+m+1过(0,
,得出直线y=mx+m+1的解析式,画出图象,再根据定义求出区域W的整点个数便可;②当直线y=mx+m+1过(0,![]() )时,区域W内有两点整点,当直线y=mx+m+1过(0,2),区域W内有3个整点,由此便可求出m的取值范围.
)时,区域W内有两点整点,当直线y=mx+m+1过(0,2),区域W内有3个整点,由此便可求出m的取值范围.
解:(1)由题干条件可得B点坐标为(2,2),代入函数y=![]() (x>0)中可得k=4.
(x>0)中可得k=4.
(2)①由m=![]() ,可得直线解析式为
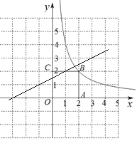
,可得直线解析式为![]() ,做出图象如下图,由图可得区域W的整点为(0,1)和(1,1),故区域W的整点个数为2个.
,做出图象如下图,由图可得区域W的整点为(0,1)和(1,1),故区域W的整点个数为2个.
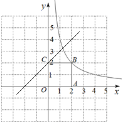
②当直线y=mx+m+1过(0,![]() )时,可得m=
)时,可得m=![]() ,此时区域W的整点个数为2个;当直线y=mx+m+1过(0,2),可得m=1,此时区域W的整点个数为3个;由图象分析可得,当直线y=mx+m+1过y轴上(0,
,此时区域W的整点个数为2个;当直线y=mx+m+1过(0,2),可得m=1,此时区域W的整点个数为3个;由图象分析可得,当直线y=mx+m+1过y轴上(0,![]() )至(0,2)之间时,区域W内有3个整点为(0,1),(1,1),(1,2),但当直线y=mx+m+1过y轴上(0,2)点之上的点时,点(1,3)会在区域W内,不符合题干要求,综上可得,区域W内恰有3个整点时,m的取值范围为
)至(0,2)之间时,区域W内有3个整点为(0,1),(1,1),(1,2),但当直线y=mx+m+1过y轴上(0,2)点之上的点时,点(1,3)会在区域W内,不符合题干要求,综上可得,区域W内恰有3个整点时,m的取值范围为![]() <m≤1.
<m≤1.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?