Question

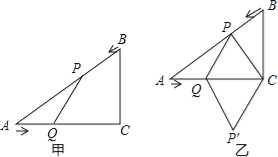
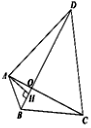
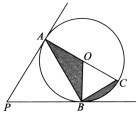
【题目】如图，PA、PB与⊙O相切，切点分别为A、B，PA＝3，∠P＝60°，若AC为⊙O的直径，则图中△OBC的面积为( )

A.B.C.D.

Answer 1

【答案】C

【解析】

首先证明△PAB和△OBC为等边三角形，可得AB＝PA＝3，∠OCB＝60°，然后利用三角函数求出BC，再根据S△AOB＝S△OBC＝进行计算．

解：∵PA、PB与⊙O相切，

∴PA＝PB，∠PAO＝∠PBO＝90°，

∵∠P＝60°，

∴△PAB为等边三角形，∠AOB＝120°，

∴AB＝PA＝3，∠BOC＝60°，

∵OB＝OC，

∴△OBC为等边三角形，

∴∠OCB＝60°，

∵AC为⊙O的直径，

∴∠ABC＝90°，

∴BC＝，

∴，

∵OA＝OC，

∴S△AOB＝S△OBC＝，

故选：C．