题目内容
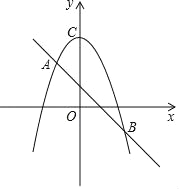
【题目】快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图像如图所示.
(1)A市和B市之间的路程是 km;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)快车与慢车迎面相遇以后,再经过多长时间两车相距20 km?

【答案】(1)360.(2)a=120,点M的横坐标、纵坐标的实际意义是两车出发2小时时,在距B市120 km处相遇.(3)快车与慢车迎面相遇以后,再经过![]() 或
或![]() h两车相距20 km.
h两车相距20 km.
【解析】
(1)由函数图象的数据意义直接可以得出A、B两地之间的距离;
(2)根据题意得快车速度是慢车速度的2倍,观察图象知2小时快车与慢车迎面相遇,列出方程可求得答案;
(3)利用待定系数法分别求出AB、BC、OC的解析式,根据题意列出方程求解即可.
(1)由题意得:A市和B市之间的路程是360 km;
(2)根据题意得快车速度是慢车速度的2倍,设慢车速度为x km/h,则快车速度为2x km/h.
根据题意,得 2(x+2x)=360,解得x=60.
2×60=120,所以a=120.
点M的横坐标、纵坐标的实际意义是两车出发2小时时,在距B市120km处相遇.
(3)快车速度为120 km/h,到B市后又回到A市的时间为![]() (h).
(h).
慢车速度为60 km/h,到达A市的时间为360÷60=6(h).
如图:

当0≤x≤3时,
设AB的解析式为:![]()
由图象得:![]() ,
,![]() ;
;![]() ,
,![]() ;代入
;代入![]() 得:
得:
![]()
解得:![]()
∴AB的解析式为:y=-120x+360(0![]() x≤3).
x≤3).
当3<x≤6时,
设BC的解析式为:![]()
由图象得:![]() ,
,![]() ;
;![]() ,
,![]() ;代入
;代入![]() 得:
得:
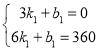
解得:
∴函数的解析式为:y1=120x-360(3<x≤6) .
设OC的解析式为:![]()
由图象得:![]() ,
,![]() ;代入
;代入![]() 得:
得:
![]()
解得:![]()
∴OC的解析式为:y2=60x(0![]() x≤6).
x≤6).
当0≤x≤3时,
根据题意,得y2-y=20,即60x-(-120x+360)=20,
解得x=![]() ,
,![]() .
.
当3<x≤6时,
根据题意,得y2-y1=20,即60x-(120x-360)=20,
解得x=![]() ,
,![]() -2=
-2=![]() .
.
所以,快车与慢车迎面相遇以后,再经过![]() 或
或![]() h两车相距20km.
h两车相距20km.