题目内容
【题目】已知关于![]() 的方程
的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() .
.
![]() 求
求![]() 的取值范围.
的取值范围.
![]() 是否存在实数
是否存在实数![]() ,使方程的两实数根互为相反数?
,使方程的两实数根互为相反数?
【答案】(1)![]() 且
且![]() ;(2)
;(2)![]() 不存在,理由见解析
不存在,理由见解析
【解析】
(1)因为方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根x1,x2.得出其判别式△>0,可解得k的取值范围;
(2)假设存在两根的值互为相反数,根据根与系数的关系,列出对应的不等式即可求出k的值.
(1)方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根x1,x2,可得:k﹣1≠0且△=﹣12k+13>0,解得:k<![]() 且k≠1;
且k≠1;
(2)假设存在两根的值互为相反数,设为 x1,x2.
∵x1+x2=0,∴﹣![]() =0,∴k=
=0,∴k=![]() .
.
又∵k<![]() 且k≠1,∴k不存在.
且k≠1,∴k不存在.

练习册系列答案
相关题目
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 |
|
|
(1)完成上表;
(2)若从盒子中随机摸出一个球,则摸到白球的概率P= ;(结果保留小数点后一位)
(3)估算这个不透明的盒子里白球有多少个?
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
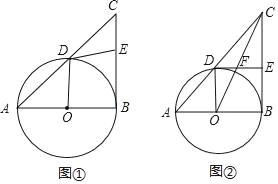
![]() 如图
如图![]() ,求证:四边形
,求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,当
,当![]() 时,取
时,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形
,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形![]() ).
).