Question

【题目】如图，直线AB、CD相交于点O，∠BOE=90°，OM平分∠AOD，ON平分∠DOE．

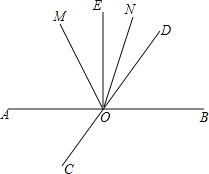
（1）若∠EON=18°，求∠AOC的度数．

（2）试判断∠MON与∠AOE的数量关系，并说明理由．

Answer 1

【答案】（1）54°；（2）∠MON=∠AOE=45°．

【解析】

试题分析：（1）直接利用角平分线的性质得出∠DOE的度数，再求出∠DOB的度数，进而得出答案；

（2）直接利用未知数表示出∠AOD、∠MOD、∠MON进而求出答案．

解：（1）∵ON平分∠DOE，

∴∠DOE=2∠EON=36°，

∵∠BOE=∠DOE+∠DOB=90°，

∴∠DOB=∠BOE﹣∠DOE=54°，

∴∠AOC=∠DOB=54°；

（2）∠DON=∠AOE

理由：设∠DON=x°，

∵ON平分∠DOE，

∴∠DOE=2∠DON=2x°，

∵∠AOE+∠BOE=180°，∠BOE=90°，

∴∠AOE=180°﹣∠BOE=90°，

∴∠AOD=∠AOE+∠DOE=（90+2x）°，

∵OM平分∠AOD，

∴∠MOD=（90+2x）°=（45+x）°，

∴∠MON=∠MOD﹣∠DON=45°，

∴∠MON=∠AOE=45°．