题目内容
【题目】如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)△BCE≌△CAD的依据是 (填字母);
(2)猜想:AD、DE、BE的数量关系为 (不需证明);
(3)当BE绕点B、AD绕点A旋转到图2位置时,线段AD、DE、BE之间又有怎样的数量关系,并证明你的结论.
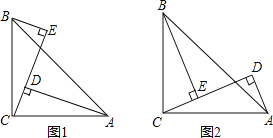
【答案】(1)AAS;(2)见解析;(3)DE=BE﹣AD.
【解析】
试题分析:(1)由题中条件求解△ACD≌△CBE,需要用到两个角和一个边;
(2)由题中条件求解△ACD≌△CBE,得出对应边相等,再利用线段之间的转化,进而可得出结论;
(3)中还是先求解△ACD≌△CBE,利用线段之间的转化得出结论.
(1)解:AAS.
(2)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,BE=CD,
DE=CE﹣CD=AD﹣BE.
(3)解:DE=CD﹣CE=BE﹣AD.
证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CD﹣CE=BE﹣AD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目