题目内容
【题目】如图,在△ABC中,∠C=90°,∠A>∠B.
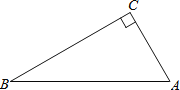
(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.
【答案】(1)见解析;(2)∠B=30°,∠BAC=60°.
【解析】
试题分析:(1)利用基本作图(作线段的垂直平分线)作出DE;
(2)先利用角平分线性质定理的逆定理得到AE平分∠DAC,即∠CAE=∠BAE,再根据线段垂直平分线的性质定理得到EA=EB,则∠B=∠BAE,所以∠BAC=2∠B,再利用互余得到∠B+∠BAC=90°,于是得到∠B=30°,∠BAC=60°.
解:(1)如图,DE为所作;
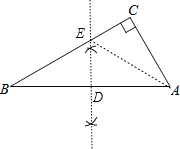
(2)连结AE,如图,
∵EC⊥AC,ED⊥AD,CE=DE,
∴AE平分∠DAC,即∠CAE=∠BAE,
∵ED垂直平分AB,
∴EA=EB,
∴∠B=∠BAE,
∴∠BAC=2∠B,
∵∠B+∠BAC=90°,
∴∠B=30°,∠BAC=60°.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目