题目内容
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.

(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论

(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论
(1)证明见解析(2) 矩形,证明见解析
证明:(1)在△ADF和△CDE中,
∵AF∥BE,∴∠FAD=∠ECD,
又∵D是AC的中点,∴AD=CD,
∵∠ADF=∠CDE,∴△ADF≌△CDE(ASA),∴AF=CE.
(2)若AC=EF,则四边形AFCE是矩形.
证明:由(1)知AF綊CE,∴四边形AFCE是平行四边形,
又∵AC=EF,∴四边形AFCE是矩形
(1)可通过全等三角形来证明简单的线段相等.△ADF和△CDE中,已知了AD=CD,∠ADF=∠CDE,AF∥BE,因此不难得出两三角形全等,进而可得出AF=CE.
(2)需先证明四边形AFCE是平行四边形,那么对角线相等的平行四边形是矩形.
∵AF∥BE,∴∠FAD=∠ECD,
又∵D是AC的中点,∴AD=CD,
∵∠ADF=∠CDE,∴△ADF≌△CDE(ASA),∴AF=CE.
(2)若AC=EF,则四边形AFCE是矩形.
证明:由(1)知AF綊CE,∴四边形AFCE是平行四边形,
又∵AC=EF,∴四边形AFCE是矩形
(1)可通过全等三角形来证明简单的线段相等.△ADF和△CDE中,已知了AD=CD,∠ADF=∠CDE,AF∥BE,因此不难得出两三角形全等,进而可得出AF=CE.
(2)需先证明四边形AFCE是平行四边形,那么对角线相等的平行四边形是矩形.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 中,点
中,点 、
、 、
、 分别在
分别在 、
、 、
、 上,
上, ,
, ,且
,且

 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 ,点
,点 重合),过点
重合),过点 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线 对折,点
对折,点 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 .
. 的度数;
的度数; 边上?
边上? ?
?
 中,
中,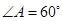 ,对角线
,对角线 ,则菱形
,则菱形
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连结
,连结 .
. ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.

 是
是 的中点,且
的中点,且 ,有下列结论:①.两三角形面积
,有下列结论:①.两三角形面积 ②.
②. ③.四边形
③.四边形 是等腰梯形 ④.
是等腰梯形 ④. 其中不正确的是_________________.
其中不正确的是_________________.
 ABCD中,AB=5,AD=8,∠BAD、∠ADC的平分线分别交BC于E、F,则EF的长为
ABCD中,AB=5,AD=8,∠BAD、∠ADC的平分线分别交BC于E、F,则EF的长为 
