题目内容
在
ABCD中，AB＝5，AD＝8，∠BAD、∠ADC的平分线分别交BC于E、F，则EF的长为
A. 1 B. 2 C. 3 D. 4
ABCD中，AB＝5，AD＝8，∠BAD、∠ADC的平分线分别交BC于E、F，则EF的长为 A. 1 B. 2 C. 3 D. 4
B
∵AF平分∠BAD，
∴∠BAF=∠DAF，
又∵AD∥CB，
∴∠AFB=∠DAF，
∴∠BAF=∠AFB，
则BF=AB=5；
同理可得，CE=CD=5．
∴EF=BF+CE﹣BC=BF+CE﹣AD=5+5﹣8=2．
故选B．
∴∠BAF=∠DAF，
又∵AD∥CB，
∴∠AFB=∠DAF，
∴∠BAF=∠AFB，
则BF=AB=5；
同理可得，CE=CD=5．
∴EF=BF+CE﹣BC=BF+CE﹣AD=5+5﹣8=2．
故选B．
练习册系列答案
相关题目
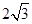
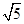
的周长比
的周长大7cm,则CD的长是 cm.