题目内容
【题目】定义：对于抛物线y＝ax2+bx+c（a、b、c是常数，a≠0），若b2＝ac，则称该抛物线为黄金抛物线．例如：y＝x2﹣x+1是黄金抛物线
（1）请再写出一个与上例不同的黄金抛物线的解析式；
（2）将黄金抛物线y＝x2﹣x+1沿对称轴向下平移3个单位
①直接写出平移后的新抛物线的解析式；
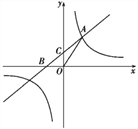
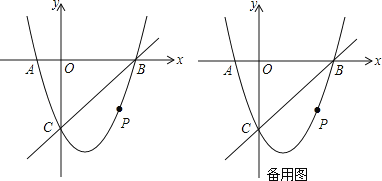
②新抛物线如图所示，与x轴交于A、B（A在B的左侧），与y轴交于C，点P是直线BC下方的抛物线上一动点，连结PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
③当直线BC下方的抛物线上动点P运动到什么位置时，四边形 OBPC的面积最大并求出此时P点的坐标和四边形OBPC的最大面积．
【答案】（1）y＝x2+x+1；（2）①：y＝x2﹣x﹣2；②存在P点的坐标为（
，﹣1）；当x＝1时，最大值是3，P（1，﹣2）
【解析】
（1）直接根据黄金抛物线的定义写一个解析式即可；
（2）①根据平移的知识直接写出新抛物线的解析式；
②设P点坐标为（x，x2﹣x﹣2），PP′交CO于E，若四边形POP′C是菱形，则有PC＝PO，连结PP′则PE⊥CO于E，P点的横坐标为﹣1，进而解方程求出x的值；
③过点P作y轴的平行线与BC交于点Q，与OB交于点F，设P（x，x2﹣x﹣2），先求出BC的直线解析式，进而设Q点的坐标为（x，x﹣2），根据S四边形OBPC=S△OBC+S△BPQ+S△CPQ列出x的二次函数解析式，根据二次函数的性质求出满足条件的P点坐标以及面积最大值．
解：（1）不唯一，例如：y＝x2+x+1；
（2）①：y＝x2﹣x﹣2；
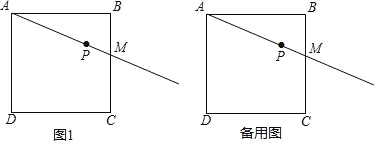
②存在点P，如图1，使四边形POP′C为菱形．
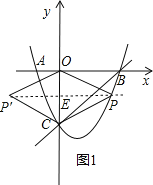
设P点坐标为（x，x2﹣x﹣2），PP′交CO于E
若四边形POP′C是菱形，则有PC＝PO．
连结PP′则PE⊥CO于E，
∴OE＝EC＝1，
∴y＝﹣1，
∴x2﹣x﹣2＝﹣1
解得x1＝，x2＝
（不合题意，舍去）
∴P点的坐标为（，﹣1）；
③过点P作y轴的平行线与BC交于点Q，与OB交于点F，如图2
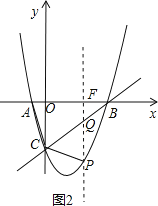
设P（x，x2﹣x﹣2），
易得，直线BC的解析式：y＝x﹣2
则Q点的坐标为（x，x﹣2）．
S四边形OBPC＝S△OBC+S△BPQ+S△CPQ
＝
OBOC+QPOF+QPFB＝
＝﹣（x﹣1）2+3，
当x＝1时，四边形OBPC的面积最大
此时P点的坐标为（1，﹣2），
四边形OBPC的面积最大值是3．
