题目内容
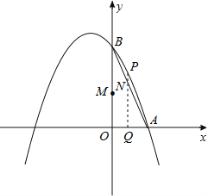
【题目】如图,抛物线经过A(-1,0),B(5,0),C(0,-![]() )三点.
)三点.
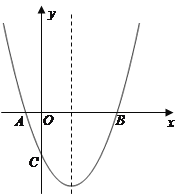
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
【答案】(1)![]() .;(2) (2,-
.;(2) (2,-![]() ).
).
【解析】试题(1)先设所求二次函数的解析式为y=ax2+bx+c(a≠0),再把A(-1,0),B(5,0),C(0,-![]() )入函数解析式,得到关于a、b、c的三元一次方程组,解即可求a、b、c,进而可得函数解析式.
)入函数解析式,得到关于a、b、c的三元一次方程组,解即可求a、b、c,进而可得函数解析式.
(2)连接BC,交对称轴于P,P即为使PA+PC的值最小,设直线BC的解析式,把B、C的坐标代入即可求得系数,进而求得解析式,令x=2时,即可求得P的坐标.
试题解析:(1)设所求二次函数的解析式为y=ax2+bx+c(a≠0),
代入A(-1,0),B(5,0),C(0,-![]() )三点,得
)三点,得
 ,
,
解得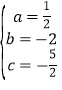 ,
,
所以这个二次函数的解析式是:![]() .
.
(2)∵![]()
=![]()
∴抛物线的对称轴为x=2,
设直线BC的解析式为y=kx+m,
∴
解得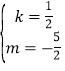 ,
,
∴直线BC的解析式为y=![]() ,
,
当x=2时,y=-![]() ,
,
∴P点的坐标为(2,-![]() ).
).

练习册系列答案
相关题目