题目内容
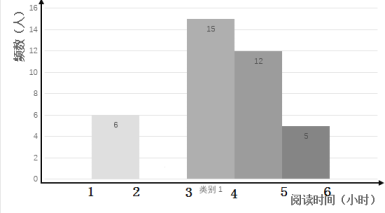
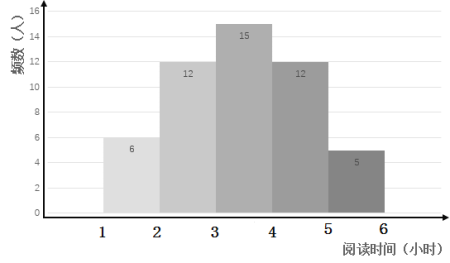
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,详见解析;(3)
,详见解析;(3)![]()
【解析】
(1)先根据![]() 的频数和频率求出样本容量,然后再运用频率、频数、总数的关系即可求出a和n的值;
的频数和频率求出样本容量,然后再运用频率、频数、总数的关系即可求出a和n的值;
(2)根据数据将频数分布直方图补充完整即可;
(3)先由题意画出树状图,然后由树状图求得所有等可能的结果与刚好抽到一名男生和一名女生的情况,再利用概率公式即可求.
解:(1)抽样的样本容量b=![]() =50,
=50,
则n=![]() =0.24
=0.24
故![]() ,
,![]() ;
;
(2)由题意得![]() ,故如图:
,故如图:
(3)由题意列树状图:

由树状图可知,在5名同学中随机抽取2名同学的所有等可能的结果有20种,恰好抽到一男一女(记为事件![]() )的结果有12种
)的结果有12种
![]() .
.

【题目】在新的教学改革的推动下,某中学初三年级积极推进走班制教学.为了了解一段时间以来“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取20名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的20名同学的数学成绩统计(满分为100分)(单位:分):86 90 60 76 92 83 56 76 85 70 96 96 90 68 78 80 68 96 85 81
“至善班”乙班的20名同学的数学成绩统计(满分为100分)(单位:分):78 96 75 76 82 87 60 54 87 72 100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
分数 数量 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
(1)完成下表:
平均数 | 中位数 | 众数 | |
甲班 | 80.6 | 82 | a= |
乙班 | 80.35 | b= | 78 |
(2)在“至善班”甲班的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数为 ,估计全部“至善班”的1600人中优秀人数为 人.(成绩大于等于80分为优秀)
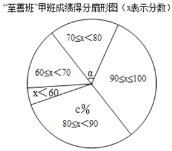
(3)根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:① ;② .