题目内容
【题目】(1)探究发现:下面是一道例题及解答过程,请补充完整:
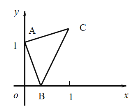
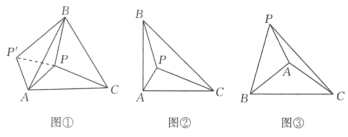
如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.
【答案】(1)P’B,P’B2;(2)2PA2+PB2=PC2,见解析;(3)k=![]()
【解析】
(1)根据旋转的性质和勾股定理直接写出即可.
(2)将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,论证PP′=2PA,再根据勾股定理代换即可.
(3)将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,论证PP′=![]() PA,再根据勾股定理代换即可.
PA,再根据勾股定理代换即可.
(1)PC=P’B,P’P2+BP2=P’B2
(2)关系式为:2PA2+PB2=PC2
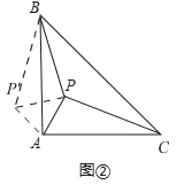
证明:将△APC绕A点逆时针旋转90°,得到△AP’B,连接PP’,则△APP’为等腰直角三角形,
∴∠APP’=45°,PP’=![]() PA,PC=P’B,
PA,PC=P’B,
∵∠APB=135°,
∴∠BPP’=90°,
∴P’P2+BP2=P’B2,
∴2PA2+PB2=PC2.
(3)k=![]()
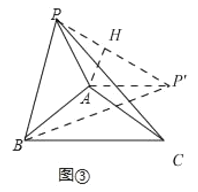
将△APC绕点A顺时针旋转120°得到△AP’B,连接PP’,过点A作AH⊥PP’,
可得![]()
![]()
![]()
![]()
![]()
![]()
![]()

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
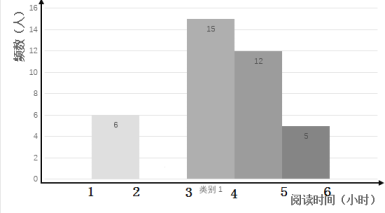
孟建平名校考卷系列答案【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.