题目内容
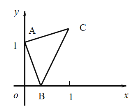
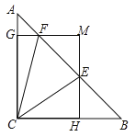
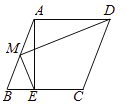
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 是锐角,
是锐角,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 的值为___________.
的值为___________.
【答案】![]()
【解析】
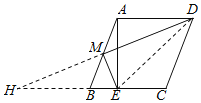
延长DM交CB的延长线于点H.首先证明△ADM≌△BHM,得出AD=HB=4,MD=MH,由线段垂直平分线的性质得出EH=ED,设BE=x,利用勾股定理构建方程求出x,即BE,结合AB得出cosB的值.
解:延长DM交CB的延长线于点H.如图所示:
∵四边形ABCD是菱形,
∴AB=BC=AD=4,AD∥CH,
∴∠ADM=∠H,
∵M是AB的中点,
∴AM=BM,
在△ADM和△BHM中,
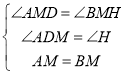 ,
,
∴△ADM≌△BHM(AAS),
∴AD=HB=4,MD=MH,
∵∠EMD=90°,
∴EM⊥DH,
∴EH=ED,
设BE=x,
∵AE⊥BC,
∴AE⊥AD,
∴∠AEB=∠EAD=90°,
∵AE2=AB2-BE2=DE2-AD2,
∴42-x2=(4+x)2-42,
解得:x=![]() ,或x=
,或x=![]() (舍),
(舍),
∴BE=![]() ,
,
∴cosB=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
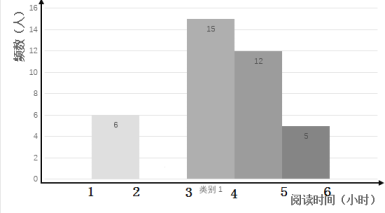
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.