��Ŀ����
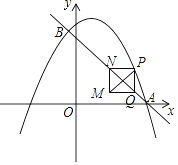
����Ŀ����ͼ����ֱ֪��y��x+2��x�ᡢy��ֱ��ڵ�A��B��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����![]() ���������߾���A��B���㣬��x������һ��C��
���������߾���A��B���㣬��x������һ��C��
��1���������ߵĽ���ʽ��
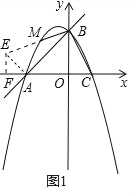
��2����M��������x���Ϸ�һ�㣬��MBA����CBO�����M�����ꣻ
��3������A��AB�Ĵ��߽�y���ڵ�D��ƽ��ֱ��AD���������ڵ�E��F���㣬����EO��FO������EFOΪ��EFΪб�ߵ�ֱ�������Σ���ƽ�ƺ��ֱ�ߵĽ���ʽ��

���𰸡���1��y����x2��x+2����2��M����![]() ��
��![]() ������3��ƽ�ƺ�Ľ���ʽΪy����x��1+
������3��ƽ�ƺ�Ľ���ʽΪy����x��1+![]() ��y����x��1��
��y����x��1��![]() ��
��
��������
��1�����ô���ϵ�������ɽ�����⣻
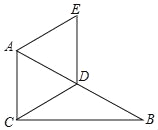
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F�������E���꣬�����ֱ��BE�Ľ���ʽ�����÷����鼴�ɽ�����⣻
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G���������������ε������Լ�����ϵ����ϵ���������鼴�ɽ�����⣻
��1����ֱ��y��x+2��x�ᡢy��ֱ��ڵ�A��B��
��A����2��0����B��0��2����
�������ߵĶԳ���x����![]() ��A��C���ڶԳ���Գƣ�
��A��C���ڶԳ���Գƣ�
��C��1��0����
�������ߵĽ���ʽΪy��a��x+2����x��1�����ѣ�0��2������õ�a����1��
�������ߵĽ���ʽΪy����x2��x+2��
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F��
�ߡ�ABE����OBC����BAE����BOC��90�㣬
���BAE�ס�BOC��
��![]() ��
��
��![]() ��
��
��AE��![]() ��
��
�ߡ�EAF+��BAO��90�㣬��BAO��45�㣬
���EAF��45�㣬
��EF��AF��1��
��E��3��1����
��ֱ��BE�Ľ���ʽΪy����![]() x+2��
x+2��
��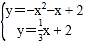 �����
�����![]() ��
��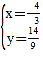 ��
��
��M��-![]() ��
��![]() ����
����
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G��
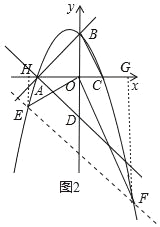
�ߡ�EOF=90��=��PHE=��OGF��
����EHO�ס�OGF�õ���
![]() ��
��
��![]() ��
��
��x1x2+y1y2=0��
��![]() ����ȥy�õ���x2+b-2=0��
����ȥy�õ���x2+b-2=0��
��x1x2=b-2��x1+x2=0��y1y2=��-x1+b����-x2+b��=x1x2+b2��
��2��b-2��+b2=0��
���b=-1-![]() ��-1+
��-1+![]() ����������
����������
��ֱ��AD����ƽ��ʱ��ͬ���ɵ�b=-1+![]() ��
��
����������ƽ�ƺ�Ľ���ʽΪy=-x-1+![]() ��y=-x-1-
��y=-x-1-![]() ��
��