题目内容
【题目】如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:①abc<0;②4a+c<2b;③![]() =1﹣
=1﹣![]() ;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=
;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=![]() 正确的是( )
正确的是( )
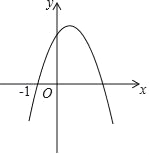
A. ①③⑤ B. ①②③④⑤ C. ①③④ D. ①②③⑤
【答案】B
【解析】
①利用图象信息即可判断;②根据x=-2时,y<0即可判断;③根据m是方程ax2+bx+c=0的根,结合两根之积-m=![]() ,即可判断;④根据两根之和-1+m=-
,即可判断;④根据两根之和-1+m=-![]() ,可得ma=a-b,可得am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,⑤根据抛物线与x轴的两个交点之间的距离,列出关系式即可判断.
,可得ma=a-b,可得am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,⑤根据抛物线与x轴的两个交点之间的距离,列出关系式即可判断.
∵抛物线开口向下,
∴a<0,
∵抛物线交y轴于正半轴,
∴c>0,
∵-![]() >0,
>0,
∴b>0,
∴abc<0,故①正确;
∵x=-2时,y<0,
∴4a-2b+c<0,即4a+c<2b,故②正确;
∵y=ax2+bx+c的图象过点(-1,0)和(m,0),
∴-1×m=![]() ,am2+bm+c=0,
,am2+bm+c=0,
∴![]() +
+![]() +
+![]() =0,
=0,
∴![]() =1-
=1-![]() ,故③正确;
,故③正确;
∵-1+m=-![]() ,
,
∴-a+am=-b,
∴am=a-b,
∵am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,故④正确;
∵m+1=|![]() -
-![]() |,
|,
∴m+1=|![]() |,
|,
∴|am+a|=![]() ,故⑤正确.
,故⑤正确.
故选:B.

【题目】为了让“两会”精神深入青年学生,增强学子们的历史使命和社会责任感,某高校党委举办了“奋力奔跑同心追梦”两会主题知识竞答活动,文学社团为选派优秀同学参加学校竞答活动,提前对甲、乙两位同学进行了6次测验:
①收集数据:分别记录甲、乙两位同学6次测验成绩(单位:分)
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
②整理数据:列表格整理两位同学的测验成绩(单位:分)
1 | 2 | 3 | 4 | 5 | 6 | |
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
③描述数据:根据甲、乙两位同学的成绩绘制折线统计图

④分析数据:两组成绩的平均数、中位数、众数、方差如下表:
同学 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 84 | 82.5 | __________ | 16.3 |
乙 | 84 | 83.5 | 83 | __________ |
得出结论:结合上述统计过程,回答下列问题:
(1)补全④中表格;
(2)甲、乙两名同学中,_______(填甲或乙)的成绩更稳定,理由是______________________
(3)如果由你来选择一名同学参加学校的竞答活动,你会选择__________(填甲或乙),理由是___________