题目内容
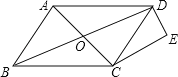
【题目】如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
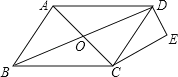
(1)求证:四边形OCED是矩形;
(2)若AD=5,BD=8,计算sin∠DCE的值.
【答案】(1)见解析;(2)sin∠DCE=![]() .
.
【解析】
试题(1)首先证明四边形OCED是平行四边形,再根据菱形的性质可得AC⊥BD,进而得到四边形OCED是矩形;
(2)首先根据菱形的性质可得![]() =4,OC=OA,AD=CD,然后再根据勾股定理可计算出DE=OC=3,再利用三角函数定义可得答案.
=4,OC=OA,AD=CD,然后再根据勾股定理可计算出DE=OC=3,再利用三角函数定义可得答案.
(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,BD=8,
∴![]() =4,OC=OA,AD=CD,
=4,OC=OA,AD=CD,
∵AD=5,
∴OC=![]() =3,
=3,
∵四边形OCED是矩形,
∴DE=OC=3,
在Rt△DEC中,sin∠DCE=![]() .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目